Поїзд мав проїхати 840 км за певний час. Але всередині шляху його було затримано на 30 хв через технічну несправність. Щоб прибути вчасно, машиністові довелося збільшити швидкість поїзда на 2 км/год. Скільки часу перебував поїзд у дорозі?
Сложение:1) при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак. П р и м е р ы : ( + 6 ) + ( + 5 ) = 11 ; 2) при сложении двух чисел с разными знаками их абсолютные величины вычитаются ( из большей меньшая ) и ставится знак числа с большей абсолютной величиной. П р и м е р ы : ( – 6 ) + ( + 9 ) = 3 ;
Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.
Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
+ · + = +
+ · – = –
– · + = –
– · – = +
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
П р и м е р :
Деление. При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении:
Пусть (км) - расстояние между озером и селом.
(км) - расстояние между озером и селом.
_______________________________________________
"Туда"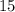
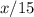

"Обратно"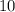
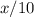

_______________________________________________
Если общий путь занял ровно час, то
час, то 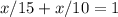 (время "туда" + время "обратно" =
(время "туда" + время "обратно" =  час).
час).
Теперь, конечно, решаем это уравнение:
Таким образом, расстояние от села к озеру (и, кстати, от озера к селу) составляет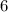 километров.
километров.
ответ: 6 километров.Вычитание. Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с обратным знаком.
Умножение. При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
+ · + = +
+ · – = –
– · + = –
– · – = +
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
П р и м е р :
Деление. При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении: