1) Обозначим искомую линейную функцию у = kx +b. По условию её график параллелен прямой y=2x+11, следовательно угловые коэффициенты этих функций равны => k = 2 => искомая функция принимает вид у = 2x +b. 2) По условию график искомой функции пересекается с графиком y=x-3 в точке, лежащей на оси ординат, значит функции у = 2x +b, y=x-3 и ось ординат OY, которая задается формулой x = 0 пересекаются в одной точке. Решаем систему: у = 2x +b y=x-3 x = 0
Получаем: b = - 3. T.о. искомая функция имеет вид: у = 2x - 3
2) По условию график искомой функции пересекается с графиком y=x-3 в точке, лежащей на оси ординат, значит функции у = 2x +b, y=x-3 и ось ординат OY, которая задается формулой x = 0 пересекаются в одной точке.
Решаем систему:
у = 2x +b
y=x-3
x = 0
Получаем: b = - 3.
T.о. искомая функция имеет вид: у = 2x - 3
а) Эллипс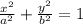 .
.
Подставляем координаты точек А и В.
(0²/a²) + ((√3)²/b²) = 1. Отсюда b = +-√3.
((√(14/3)²/a²) + (1²/b²) = 1 подставим b = +-√3.
((14/3)/a²) + (1/3) = 1,
((14/3)/a²) = 2/3,
3a² = 21,
а = +-√7.
ответ: уравнение эллипса (x²/(√7)²) + (y²/(√3)²) = 1.
б) Гипербола.
Так как в задании в уравнениях асимптот b = 0, то центр гиперболы в начале координат.
Уравнение асимптот: у = +-(b/a)x = √21/10.
Так как b/а = √21/10 дано в задании, то сразу имеем значения полуосей: а = 10, b = √21 и получаем уравнение гиперболы:
(x²/(10²) - (y²/(√21)²) = 1.
Проверим значения а и b по заданному эксцентриситету: b²/a² = ε² - 1.
Получаем: 21/100 = 121/100 - 1 = 21/100.
Значит, уравнение верно составлено.
в) Парабола.
Уравнение директрисы для параболы, у которой фокальная ось совпадает с осью Oy, имеет вид у = -р/2, а уравнение параболы имеет вид: x²=2py.
Директриса: у = -4 = -р/2, отсюда р = 8.
Получаем уравнение параболы: x²=2*8y.