Поезд должен был пройти 240 км за определенное время. после 3 часов пути он был задержан на 30 мин, и чтобы прибыть на место назначения без опоздания, ему пришлось увеличить скорость на 7/3 км/час. какова была первоначальная скорость поезда?
0,25^(2+0,5x^2)=0,5^2(2+0,5x^2)=0,5^(4+x^2), отсюда следует что степень числа 0,5 никогда не будет отрицательным числом и никогда не будет меньше 4. Отсюда следует, что x<1(Так как 0,25 или 0,5 в любой положительной степени будет меньше 1 а 32^1>1 32^2>1 и тд)Мало того, основываясь на этих рассуждениях можно понять что при положительной степени и нуле 32>=1, следовательно x - неположителен(напоминаю про то что 0,25 не может быть 1 в положительной степение)Получаем что x<0Подставим самое большое значение(целое). Это -1Получим: 0,5^(4+1) и 32^(-1)0,5^5 и 32^(-1)0,03125 и 1/32 = 0,03125Следовательно при -1 значения равныПодставив -2 получим верное неравенствоответ: x=-2
sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(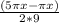
)cos(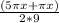
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}