Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
соня7891
16.05.2020 07:35 •
Алгебра
полное решение со всеми пояснениями действий решений показательного уравнения:
Показать ответ
Ответ:
jimjimkim
15.10.2020 16:27
0,0
(0 оценок)
Ответ:
goe1
15.10.2020 16:27
ответ:
;
Объяснение:
Найдём область допустимых значений.
ОДЗ:
Упростим уравнение.
Извлечём квадратный корень из обеих частей уравнения, не забывая об использовании положительных и отрицательных корней.
Разделим уравнение на 2 возможных случая.
Решим относительно
.
0,0
(0 оценок)
Популярные вопросы: Алгебра
Kirillik17091
04.12.2021 05:47
Винесiть множник с пiд знака корення √63...
Hause1
12.06.2020 14:30
Если это сокращается ,сократите Если это сокращается ,сократите...
динара1316
12.06.2020 14:30
Вариант ответа 1! Заранее спс......
thero10
07.05.2021 22:04
Решить уравнение х²-2/х-7=35/х-7...
KristheMalen
14.02.2020 11:40
Преобразуй дроби a (в 4 степени) /13m и c/m (во 2 степени) так, чтобы получились дроби с одинаковыми знаменателями....
катя4842
13.06.2020 05:55
Sos! I vas proshu. Вариантов ответа несколько...
RedZilla54
15.02.2020 03:14
Одна сторона треугольника на 9 см меньше второй и вдвое меньше третьей. Найдите стороны треугольника, если периметр равен 105 см. Указание. 1 сторона - на 9 см меньше вдвое меньше...
rusnazasly
15.02.2020 03:14
Вариантов ответа несколько Вариантов ответа несколько :) >...
nshexovceva18
14.02.2023 21:54
Найдите значения выражения (√8+√2)×(√8-√2)+√8×√32=...
Eva5768
17.07.2022 06:34
Решить уравнение f `(x)=a, если: f(x)=3e^(x+4), а=3/e...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
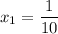 ;
; 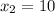
Объяснение: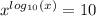
Найдём область допустимых значений.ОДЗ: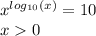
Упростим уравнение.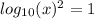
Извлечём квадратный корень из обеих частей уравнения, не забывая об использовании положительных и отрицательных корней.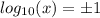
Разделим уравнение на 2 возможных случая.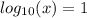
Решим относительно