При любом а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии
Объяснение:
Решение в приложении
У кубической параболы будет всего один центр симметрии. В точке с абсциссой ординатой . Эта точка совпадает с точкой перегиба.
Если посмотреть скриншоты, то только в случае выполняется условие центра симметрии.
Это можно было бы доказать с параллельного переноса, растяжения и сжатия, поворота кубической параболы y=x³. Любая другая парабола получается из исходной с этих преобразований.
Интересно еще вот что, в формуле Кардано для решения кубического уравнения первая подстановка именно .
1. Для начала можно заметить, что сумма S1=х1..х100=1 - некоторая ломаная линия, длиной 1.
А S2=х1*х2...+х99*х100 - некоторое количество сумм площадей прямоугольников, со сторонами суммы сверху.
Так вот, сумму S1 можно изобразить в виде ломаной, где нечетные х - это вертикальные линии, а четные - смежные с предыдущими горизонтальные линии.
Теперь S1 будет выглядеть как "ступеньки". А S2 - это прямоугольники, отсекаемые вертикальной и горизонтальной линией( нечетные номера произведений S2) - лежащие снизу "ступенек", - или прямоугольники, отсекаемые горизонтальной и вертикальной линией( четные номера произведений S2).
2. Известно, что максимальное значение х1*х2 , при известном постоянном х1+х2 будет достигаться когда х1=х2, то есть прямоугольник будет квадратом. Так как максимальная площадь из множества прямоугольников с одинаковым периметром будет у квадрата.
Из S1 следует, что максимальное значение для х1=х2=1/2
Теперь пусть взяв А и построив от нее вертикально х1 и горизонтально х2 мы придем в точку В. Очертим квадрат со стороной х1=х2=1/2 и вершинами в А и В.
3. Теперь вспомним о наших "ступеньках":
пусть начало их в точке А, а конец в точке С. Тогда А-С образуют прямоугольник внутри которого будут расположены площади S2, причем полупериметр А-С = 1. Но наш квадрат А-В будет иметь не меньшую площадь чем А-С, а значит не меньшую площадь чем все возможные площади прямоугольников из суммы S2.
При любом а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии
Объяснение:
Решение в приложении
У кубической параболы будет всего один центр симметрии. В точке с абсциссой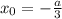
ординатой 
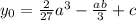. Эта точка совпадает с точкой перегиба.
Если посмотреть скриншоты, то только в случае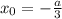
выполняется условие центра симметрии.
Это можно было бы доказать с параллельного переноса, растяжения и сжатия, поворота кубической параболы y=x³. Любая другая парабола получается из исходной с этих преобразований.
Интересно еще вот что, в формуле Кардано для решения кубического уравнения первая подстановка именно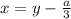
.
1. Для начала можно заметить, что сумма S1=х1..х100=1 - некоторая ломаная линия, длиной 1.
А S2=х1*х2...+х99*х100 - некоторое количество сумм площадей прямоугольников, со сторонами суммы сверху.
Так вот, сумму S1 можно изобразить в виде ломаной, где нечетные х - это вертикальные линии, а четные - смежные с предыдущими горизонтальные линии.
Теперь S1 будет выглядеть как "ступеньки". А S2 - это прямоугольники, отсекаемые вертикальной и горизонтальной линией( нечетные номера произведений S2) - лежащие снизу "ступенек", - или прямоугольники, отсекаемые горизонтальной и вертикальной линией( четные номера произведений S2).
2. Известно, что максимальное значение х1*х2 , при известном постоянном х1+х2 будет достигаться когда х1=х2, то есть прямоугольник будет квадратом. Так как максимальная площадь из множества прямоугольников с одинаковым периметром будет у квадрата.
Из S1 следует, что максимальное значение для х1=х2=1/2
Теперь пусть взяв А и построив от нее вертикально х1 и горизонтально х2 мы придем в точку В. Очертим квадрат со стороной х1=х2=1/2 и вершинами в А и В.
3. Теперь вспомним о наших "ступеньках":
пусть начало их в точке А, а конец в точке С. Тогда А-С образуют прямоугольник внутри которого будут расположены площади S2, причем полупериметр А-С = 1. Но наш квадрат А-В будет иметь не меньшую площадь чем А-С, а значит не меньшую площадь чем все возможные площади прямоугольников из суммы S2.
То есть maxS2=1/4 -!