Алгебра: Постройте график функции: y=x²-12x+4

Постройте график функции: y=x²-12x+4

Показать ответ

Ответ:

ddawka

20.07.2020 22:15

1) Аналитический.

2) Рекуррентній.

3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...

4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.

$y_n=2^n\\y_4=2^4=16$

$a_n=4n-9\\a_1=4 \cdot 1-9=-5\\a_2=4 \cdot 2-9=-1\\a_3=4 \cdot 3-9=3\\$

7) Это арифметическая прогрессия.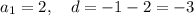 $a_1=2, \quad d=-1-2=-3$

a_n=a_1+d(n-1)=2-3(n-1)=2-3n+3=5-3n.

$d_n=2n^2-5=5\\2n^2=10\\n^2=5\\n=\sqrt{5}$

ответ: нет, не является, потому что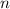 должно быть натуральным числом.

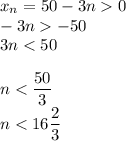
9) $x_n=50-3n0\\-3n-50\\3n$

Наибольшее натуральное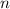 , удовлетворяющее этому неравенству, — это 16.

ответ: 16 членов.

10)

$b_n=0{,}125(n-15)^2=200\\b_n=\frac 18(n-15)^2=200\\(n-15)^2=1600\\(n-15)^2=40^2\\(n-15)= \pm 40\\n_1=40+15=55\\n_2=-40+15=-25$

Второе решение не подходит, поскольку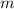 должно быть натуральным числом.

ответ: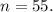 n=55.

0,0(0 оценок)

Ответ:

098473

12.03.2021 07:32

2) как известно все углы прямоугольника прямые. <А=<В=<С=<D=90`

С диагоналей разбивает их на прямоугольные треугольники ACD и АВС .

угол ACD равен 60' по условии задачи . А угол D =90' => угол CAD=30'. Итак все углы треугольника АСD известны теперь переходим на треугольник АВО. Т .к. угол А =90' в угол САD=30' угол ВАО=60' . Угол ВЕА =90' в угол BAO=60' значит угол ABE=30'=ЕВО.

По условии задачи ОЕ=4см . По условии прямоугольного треугольника :если один из углов треугольника равен 30' то противоположный катет равен половине гипотенузы. В нашем случае катет лежащий противоположно углу ЕВО=30' это ОЕ=4см

Отсюда следует что гипотенуза ВО=2ОЕ=2×4=8 . Так как точка О середина отрезка BD то ВD=2 ×BO=2×8=16

B прямоугольника диагонали равны значит диагональ АС=ВD= 16 см

Объяснение:

$1) \sqrt{9 + 2 \sqrt{20} } - \sqrt{9 - 2 \sqrt{20} } \\ 2 \sqrt{20} = 2( \sqrt{5} \times \sqrt{4} ) \\ { \sqrt{5} }^{2} + { \sqrt{4} }^{2} = 5 + 4 = 9 \\ \sqrt{9 + 2 \sqrt{20} } = \sqrt{ {( \sqrt{5} + \sqrt{4} )}^{2} } \\ \sqrt{9 - 2 \sqrt{20} } = \sqrt{ {( \sqrt{5} - \sqrt{4} ) }^{2} } \\ \sqrt{5} + \sqrt{4} - ( \sqrt{5} - \sqrt{4} ) = \sqrt{5} + \sqrt{4} - \sqrt{5} + \sqrt{4} = 2 + 2 = 4$