Рассмотрим функцию . Её производная функции: . Приравнивая производную функции к нулю, мы получим
которое равносильно уравнению откуда
_____-____(1)____+_____
Функция убывает на промежутке t ∈ (-∞; 1), а возрастает - t ∈ (1; +∞). Следовательно, t = 1 — относительный минимум. Тогда f(1) = 2 и при этом . То есть, t = 1 — решение уравнения и единственно.
Выполним обратную замену:
Дискриминант отрицателен, следовательно, квадратное уравнение действительных корней не имеет.
Рассмотрим первую дробь; число семь делится только на 1 и на 7, собственно поэтому мы не можем сократить эту дробь; если числитель не сокращается, то нет смысла думать о знаменателе.
Также и с двумя другими дробями: один делится только на 1, а в третьей дроби там семь , как мы говорили, делится только на 1 и 7, так что не смысла думать об числителе,
Так как, если один из них (знаменатель/числитель) не сокращается, то сразу же делаем вывод, что дробь не сокращается. У этих дробей нет наибольшего общего знаменателя, а без него дробь не сокращается.
Пусть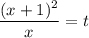 , тогда мы получаем
, тогда мы получаем
Рассмотрим функцию . Её производная функции:
. Её производная функции: 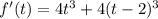 . Приравнивая производную функции к нулю, мы получим
. Приравнивая производную функции к нулю, мы получим
_____-____(1)____+_____
Функция убывает на промежутке t ∈ (-∞; 1), а возрастает - t ∈ (1; +∞). Следовательно, t = 1 — относительный минимум. Тогда f(1) = 2 и при этом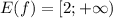 . То есть, t = 1 — решение уравнения
. То есть, t = 1 — решение уравнения 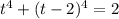 и единственно.
и единственно.
Выполним обратную замену:
Дискриминант отрицателен, следовательно, квадратное уравнение действительных корней не имеет.
ответ: нет решений.
Нет, эти правильные дроби не сокращаются
Рассмотрим первую дробь; число семь делится только на 1 и на 7, собственно поэтому мы не можем сократить эту дробь; если числитель не сокращается, то нет смысла думать о знаменателе.
Также и с двумя другими дробями: один делится только на 1, а в третьей дроби там семь , как мы говорили, делится только на 1 и 7, так что не смысла думать об числителе,
Так как, если один из них (знаменатель/числитель) не сокращается, то сразу же делаем вывод, что дробь не сокращается. У этих дробей нет наибольшего общего знаменателя, а без него дробь не сокращается.