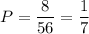Представьте в виде многочлена степень: (а2-b2) 3(m2+n2) 3(2a2+b2) 3

1). На 9 делятся те натуральные числа, сумма цифр которых кратна 9. Например:
1179 (1 + 1 + 7 + 9 = 18, 18 : 9 = 2).
2). На 3 делятся все натуральные числа, сумма цифр которых кратна 3. Например:
39 (3 + 9 = 12; 12 : 3 = 4);
3). На 2 делятся все четные натуральные числа, например: 172, 94,67 838, 1670.
4). На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0. Например: 125; 10 720.
5).На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4. Например:
124 (24 : 4 = 6);
103 456 (56 : 4 = 14).

Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 шара из 8:

Количество благоприятных исходов:

а) Подсчитаем сколькими можно вынуть 3 красных шара.

это можно сделать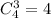

Вероятность того, что все 3 шарика красные, равна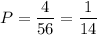

б) Подсчитаем сколькими можно вынуть 2 шарика красного цвета и 1 желтого. Красных 2 шарика можно выбрать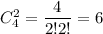 а 1 желтого По правилу произведения, таких

Вероятность того, что среди выбранных 3 шаров будет 2 красного цвета и 1 желтого, равна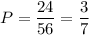

в) Подсчитаем сколькими можно выбрать 3 шарика одного цвета. Три красных шара мы посчитали в пункте а таких 4, аналогично, выбрать три желтых шара можно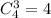 По правилу сложения, таких

Вероятность того, что среди трех выбранных шаров будет все шарики одного цвета, равна