Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина? часов. А легковая, соответственно, часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на часа раньше, значит, в целом она пробыла в пути на часов меньше.
- разница во времени.
Составим уравнение:
.
Избавимся от знаменателей, умножив обе части на общий множитель 3х.
ну графики ты сама построишь если умеешь строить графики линейных функций
а находить координаты пересечений без графика надо с системы
y=-4x+1 { - объединение в систему функций
{
y=2x-3 |вторую функцию умножаем на 2 чтобы решить путём сложения
y=-4x+1
{
2y=4x-6 умножаем 2 функцию yf 2 для решения путём сложения -4x и 4x сокращаются
3y=-5
y=-5/3 (дробь впереди со знаком -)
подставляем значение y в любую из фукций системы например в 1 и решаем
-5/3=-4x+1
4x-1=5/3
4x=8/3
x=2/3
для проверки попробуем подставить во вторую функцию
-5/3=2x-3
-2x+3=5/3
-2x=-4/3
x=2/3
точка пересечения (2/3; -5/3)
надеюсь в задаче те надо было найти точку пересечения без графиков
Скорость грузовой машины - 40км/ч.
Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина?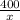
часов. А легковая, соответственно, 
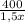часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на 
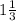часа раньше, значит, в целом она пробыла в пути на 
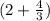часов меньше.
Составим уравнение:
Избавимся от знаменателей, умножив обе части на общий множитель 3х.
Получим: 800 = 1200 - 10х
10х=400
х=40.
А это и есть скорость грузовика