Согласно свойству арифметической прогрессии: d = a3 - a2 и одновременно d = a2 - a1. Поэтому a3 - a2 = a2 - a1. Итак, a3 = 2a2 - a1.
√(12х+13) = 2√(5х+4) - √х
ОДЗ:
1. 12х+13≥0; х≥-1 1/12
2. 5х+4≥0; х≥-4/5
3. х≥0
ОДЗ: х≥0
(√(12х+13))^2 = (2√(5х+4) - √х)^2
12х+13 = 4(5х+4)-4√(5х+4)√х+х
12х+13 = 20х+16-4√(5х^2+4х)+х
9х+3 = 4√(5х^2+4х)
(9х+3)^2 = (4√(5х^2+4х))^2
81х^2+54х+9 = 16(5х^2+4х)
81х^2+54х+9 = 80х^2+64х
х^2-10х+9 =0
(х-1)(х-9) = 0
х = 1
х = 9
ответ: при х = 1 или х = 9.
- общее ОДЗ.
1) Проверим
;
Числа 1; 3; 5; или образуют арифметическую прогрессию.
2) Проверим
Числа 3; 7; 11; или образуют арифметическую прогрессию.
ответ: {1; 9}
Согласно свойству арифметической прогрессии: d = a3 - a2 и одновременно d = a2 - a1. Поэтому a3 - a2 = a2 - a1. Итак, a3 = 2a2 - a1.
√(12х+13) = 2√(5х+4) - √х
ОДЗ:
1. 12х+13≥0; х≥-1 1/12
2. 5х+4≥0; х≥-4/5
3. х≥0
ОДЗ: х≥0
(√(12х+13))^2 = (2√(5х+4) - √х)^2
12х+13 = 4(5х+4)-4√(5х+4)√х+х
12х+13 = 20х+16-4√(5х^2+4х)+х
9х+3 = 4√(5х^2+4х)
(9х+3)^2 = (4√(5х^2+4х))^2
81х^2+54х+9 = 16(5х^2+4х)
81х^2+54х+9 = 80х^2+64х
х^2-10х+9 =0
(х-1)(х-9) = 0
х = 1
х = 9
ответ: при х = 1 или х = 9.
ОДЗ:
1) Проверим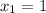
Числа 1; 3; 5; или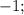
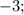
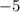 образуют арифметическую прогрессию.
образуют арифметическую прогрессию.
2) Проверим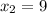
Числа 3; 7; 11; или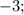
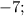
 образуют арифметическую прогрессию.
образуют арифметическую прогрессию.
ответ: {1; 9}