(см. объяснение)
Объяснение:
Выполним преобразования:
Сделаем замену вида .
Тогда уравнение примет вид:
Вернемся к записи .
Заметим, что:
Тогда, чтобы исходное уравнение имело три решения, нужно чтобы корнями уравнения были и любое .
Опираясь на этот вывод, выполним необходимые вычисления:
При :
Итого при исходное уравнение имеет ровно три различных корня.
Задание выполнено!
(см. объяснение)
Объяснение:
Выполним преобразования:
Сделаем замену вида .
.
Тогда уравнение примет вид:
Вернемся к записи .
.
Заметим, что:
ЕслиТогда, чтобы исходное уравнение имело три решения, нужно чтобы корнями уравнения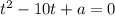 были
были 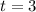 и любое
и любое 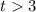 .
.
Опираясь на этот вывод, выполним необходимые вычисления:
При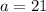 :
:
Итого при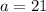 исходное уравнение имеет ровно три различных корня.
исходное уравнение имеет ровно три различных корня.
Задание выполнено!