При каком значении а уравнение имеет бесконечно много корней
а) (а+2)x=6а+12

б) (а-3)x=2а-4

в) ах-4х=а^2-16

г) 5аx-2x=-(2-5а)

Показать ответ

Ответ:

gulitenko

31.01.2020 09:43

Объяснение:

(n+6)²=n²+12n+36

(13h+1)²=169h²+26h+1

(4-3y)²=16-24y+9y²

(2k-8)²=4k²-32k+64

(3c+7d)²=9c²+42cd+49d²

(9a+t)²=81a²+18at+t²

(k-8)²=k²-16k+64

(5-7m)²=25-70m+49m²

(13p-3)²=169p²-96p+9

(2f-10a)²=4f²-40af+100f²

(-3h+7)²=9h²-42h+49

(-10x-y)²=100x²+20xy+y²

(с-10)²=c²-28c+100

(11х+4)²=121x²+88x+16

(6+2y)²=36+24y+4y²

(4k-3)²=16k²-24k+9

(3c+2d)²=9c²+12cd+4d²

(8х-3у)²=64x²-48xy+9y²

(3а-5в)²=9a²-30aв+25в²

(7с-2m)²=49с²-28сm+4m²

(в+8)²=a²+16a+64

(12h+2)²=144h²+48h+4

(5-2y)²=25-20y+4y²

(3k-4)²=9k²-24k+16

(2c+5d)²=4c²+20cd+25d²

(8a+2t)²=64a²+32at²+4t²

0,0(0 оценок)

Ответ:

morozandrey7474

05.10.2021 01:22

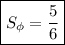3) $\boxed{S_{\phi} = \dfrac{5}{6}}$ квадратных единиц

4)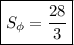 $\boxed{S_{\phi} = \dfrac{28}{3}}$ квадратных единиц

Объяснение:

По условию фигура ограничена линиями:

$y = x^{2}$

y = 0

y = -x + 2

Линии ограничивают область (закрашенную желтым цветом и которую можно назвать ABC).

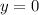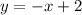Прямые y = 0 и y = -x +2 имеют пересечения в точке C(2;0).

0 = -x + 2 ⇒ x = 2; y(-2) = 0

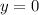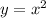Прямые y = 0 и $y = x^{2}$ имеют пересечения в точке A(0;0).

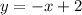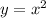Прямые y = -x + 2 и $y = x^{2}$ имеют пересечения в точке B(0;0).

$-x + 2 = x^{2}$

$x^{2} + x - 2 = 0$

$D = 1 - 4 \cdot 1\cdot (-2) =1 + 8 = 9 = 3^{2}$

$x_{1} = \dfrac{-1 + 3}{2} = \dfrac{2}{2} = 1$

$x_{2} = \dfrac{-1 -3}{2} = \dfrac{-4}{2} = -2$

Однако так как нас согласно расположению графиков относительно друг друг друга, то нас интересует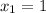 $x_{1} = 1$ , то есть точка B(1;1).

Проведем прямую x = 1. Таким образом она разбила желтую часть на две фигуры. Где площадь криволинейно трапеции ABD с пределами интегрирования от 0 до 1 можно найти с определенного интеграла, а оставшуюся площадь, как площадь треугольника BDC. То есть площадь фигуры имеет вид: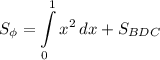 $S_{\phi} = \displaystyle \int\limits^1_0 {x^{2} } \, dx + S_{BDC}$ .

а)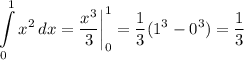 $\displaystyle \int\limits^1_0 {x^{2} } \, dx = \dfrac{x^{3}}{3} \bigg | _0^1 = \dfrac{1}{3}(1^{3} - 0^{3}) = \dfrac{1}{3}$ квадратных единиц.

б)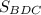 $S_{BDC}$

Так как отрезок BD треугольника ΔBDC лежит на прямой x = 1, то треугольник ΔBCD - прямоугольный с катетами BD и DC.

Зная координаты точек B(1;1),D(1;0),C(2;0) найдем длинны отрезков BD и DC.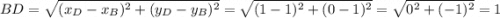 $BD = \sqrt{(x_{D} - x_{B})^{2} + (y_{D} - y_{B})^{2}} = \sqrt{(1 - 1)^{2} + (0 - 1)^{2}} = \sqrt{0^{2} + (-1)^{2}} = 1$ .

$DC = \sqrt{(x_{C} - x_{D})^{2} + (y_{C} - y_{D})^{2}} = \sqrt{(2 - 1)^{2} + (0 - 0)^{2}} = \sqrt{1^{2} + 0^{2}} = 1$ .

По формуле площади прямоугольного треугольника (ΔBDC) :

$S_{BDC} = 0,5 \cdot BD \cdot CD = 0,5 \cdot 1 \cdot 1 = 0,5$ квадратных единиц.

в) Площадь фигуры: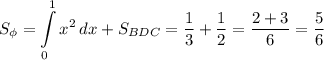 $S_{\phi} = \displaystyle \int\limits^1_0 {x^{2} } \, dx + S_{BDC} = \dfrac{1}{3} + \dfrac{1}{2} = \dfrac{2 + 3}{6} = \dfrac{5}{6}$ квадратных единиц.

По условию фигура ограничена линиями:

$y = 2\sqrt{x}$

y = 0

x = 1

x = 4

Пределы интегрирования:

a = 1

b = 4

Найдем площадь криволинейной трапеции по определению:

$S_{\phi} = \displaystyle \int\limits^4_1 {2\sqrt{x} - 0 } \, dx = \displaystyle 2 \int\limits^4_1 {\sqrt{x} } \, dx = \dfrac{4x\sqrt{x} }{3} \bigg | _4^1 = \dfrac{4}{3} (4\sqrt{4} - 1\sqrt{1)} = \dfrac{4}{3}(4 \cdot 2 - 1 \cdot 1)=$