(Профильная математика)
Найдите наибольшее значение функции y=(x+20)^2*e^-18-x на отрезке [-19;-17]

Напишите решение полностью!...

Показать ответ

Ответ:

E1hwe

07.05.2022 03:27

скорость велосипедиста 27 3/11 км/ч

Объяснение:

пусть скорость первого автобуса V₁ км/ч;

скорость второго ("быстрого") автобуса V₂ км/ч;

скорость велосипедиста Vв км/ч, тогда:

через 1/3 часа (с 8-50 до 20 мин или 1/3 часа) встретились второй автобус и велосипедист. Они расстояние:

велосипедист: Sв=Vв/3 км;

второй автобус: S₂=V₂/3=12V₁/3=4V₁ км.

Т.к. расстояние между городами 100 км, то Sв+S₂=100 км;

Vв/3+4V₁=100;

Vв=3(100-4V₁)=300-12V₁.

Получили одно уравнение с двумя переменными. Исключим переменную V₁, учитывая, что велосипедист и автобус первый встретились через 2 часа. За 2 часа они :

велосипедист: Sв=2Vв; Sв=2(300-12V₁) км;

автобус первый: S₁=2V₁ км;

сумма этих расстояний опять-таки равна 100 км:

2(300-12V₁) +2V₁ =100;

-24V₁+2V₁=100-600;

-22V₁=-500;

V₁=500/22=250/11 [км/ч]

Vв=300-12V₁; Vв=300-12*250/11=300-272 8/11=27 3/11 [км/ч]

0,0(0 оценок)

Ответ:

Пикачу1111111111

23.05.2023 10:24

ответ.

Область определения функции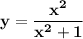 $\bf y=\dfrac{x^2}{x^2+1}$ - множество всех

действительных чисел ,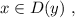 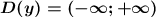$x\in D(y)\ ,$ $\boldsymbol{D(y)=(-\infty ;+\infty )}$ , так как знаменатель дроби не обращается в 0 ни при каких значениях переменной х .

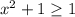Заданная функция принимает только неотрицательные значения, так как эта функция в числителе имеет выражение $x^2\geq 0$ , а в знаменателе $x^2+1\geq 1$ .

Минимальное значение, которое принимает функция, равно 0 при х=0 .

Максимальное значение стремится к 1 , так как

$\dfrac{x^2}{x^2+1}=\dfrac{x^2+1-1}{x^2+1}=1-\dfrac{1}{x^2+1}$ .

От 1 отнимается очень маленькое положительное значение , причём, чем больше значение х , тем меньшая величина вычитается . Значения, равное 1 , функция никогда не достигнет, но стремится к этому . Прямая у=1 является горизонтальной асимптотой графика . График показан на рисунке .

Поэтому область значений функции -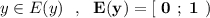 $y\in E(y)\ \ ,\ \ \bf E(y)=[\ 0\ ;\ 1\ )$ .