Промежуточная итоговая аттестация по алгебре. 8 класс.
Часть 1
1. ( ) Найдите значение выражения: 9*-25*(-1/5 )
1) 6 2) 6,6 3) 3 4) 18
2. ( ) Решите уравнение: x/4-(x-3)/5=-1
1) -8 2) 32 3) 16 4) -32
3. ( ) Какое из данных уравнений имеет единственный корень?
1) 3х^2+5х+2=0 2) х^2-9=0 3) х^2-х+1=0 4) 4х^2-12х+9=0
4. ( ) У выражение
1) 1; 2) ; 3) ; 4) 2.
5. ( ) Найдите значение выражения (a^(-11) a^3)/a^(-6) при a = 2.
6. ( ) Установите соответствие между графиками и формулами, которые их задают:
Графики
Формулы
А Б В
ответ
7. ( ) Решить неравенство
1) (− ∞; 8); 2) (− ∞;1); 3) (8; +∞); 4) (1; +∞).
Часть 2
8. ( ) Решить уравнение: x^2 + 6x + 8 = 0.
9. ( ) Решите уравнение: (2х^2-4)/х=х
б. значение аргумента при у=-5:
-2х+5 = -5 2х = 10 х = 5.
в. Чтобы узнать, принадлежит ли графику функции точки А(1;3)В(-1;6), надо подставить в формулу значение аргумента х1 = 1, х2 = -1 и сравнить значение функции и ординату точки.
Если совпадают - то точка принадлежит графику функции.
у1 = -2*1 + 5 = -2 + 5 = 3 - совпадают.
у2 = -2*(-1) + 5 = 2 + 5 = 7 - не совпадают.
2) График функции У=3х+4 - это прямая линия.
Координаты точек пересечения графика с осями координат определяются приравниванием х или у нулю.
3*0+4 = 4 = точка пересечения оси ординат (ось у)
3х+4 = 0 3х = -4 х = -4/3 = -1(1/3) - точка пересечения оси абсцисс (ось х).
3) График функции у=кх проходит через начало координат.
Коэффициент к = dy/dx = -6 / 2 = -3.
График проходит через 0 и заданную точку.
4) Точка пересечения графиков определяется решением уравнения
-4х +1,3 = х - 2,7
5х = 4
х = 4/5 = 0,8
Вторая координата находится подстановкой полученного значения х в формулу одной из прямых у = -4*0,8 + 1,3 = -3,2 + 1,3 = -1,9
или у = 0,8 - 2,7 = -1,9.
5) Параллельные графики имеют равные коэффициенты при х:
графику У=-3х+12 параллельна прямая У=3х-5.
1. x₁ = -10; x₂ = 9
2. х₁ = 8; x₂ = 6
Объяснение:
1. Решаем через дискриминант:
х²+х-90=0;
D = b²- 4ac (формула дискриминанта)
D = 1² - 4 · 1 · (-90) = 1 + 360 = 361 (Дискриминант больше нуля (361 > 0) значит у уравнения 2 корня)
√361 = 19
х₁ =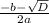
x₁ =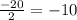
х₂ =
x₂=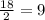
x₁ = -10; x₂ = 9
2. Решаем через дискриминант:
х²-10х-24=0
D = b²- 4ac (формула дискриминанта)
D = -10² - 4 · 1 · 24 = 100 - 96 = 4 (Дискриминант больше нуля (4 > 0) значит у уравнения 2 корня)
√4 = 2
х₁ =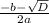
х₁ =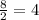
х₂ =
х₂ =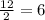
х₁ = 8; x₂ = 6
Надеюсь с: (Если что не понял пиши в комменты)