Прямая y=kx+b проходит через точки А(3:1) і B (1:5). Напишіть ривняння цієї прямо у меня 10мин осталось!

Второй объем меньше первого на 15,3 %

Объяснение:

Изначально радиус конуса r был 100%. Теперь же его увеличили на 10%, и теперь радиус конуса r₂ равен 110%. Так же это можно записать как:

r₂ = 1,1 × r

Теперь к высоте. С ней все тоже самое, только уменьшили. Значит h = 100%, a h₂ = 70%. То есть h₂ = 0,7 × h

Подставляем новые данные в формулу:

V₂ =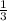 × π × (1,1 × r)² × 0,7 × h = 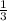× π × 1,21r² × 0,7h

Теперь если поделить V₂ на V₁ (V₁ =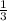 × π × r² × h), то получим 0.847, в столько раз второй объем меньше чем первый, или же это можно записать как 100% - 84,7% = 15,3 %

В решении.

Объяснение:

835.

Решить уравнение:

9/(x - 11) + 11/(x - 9) = 2

Умножить все части уравнения на (х - 11)(х - 9), чтобы избавиться от дробного выражения:

9 * (x - 9) + 11 * (x - 11) = 2*(х - 11)(х - 9)

Раскрыть скобки:

9х - 81 + 11х - 121 = 2х² - 18х - 22х + 198

20х - 202 = 2х² - 40х + 198

-2х² + 40х + 20х - 202 - 198 = 0

-2х² + 60х - 400 = 0

Разделить уравнение на -2 для упрощения:

х² - 30х + 200 = 0, квадратное уравнение, ищем корни:

ОДЗ: х ≠ 11;  х ≠ 9;

D=b²-4ac = 900 - 800 = 100        √D=10

х₁=(-b-√D)/2a  

х₁=(30-10)/2

х₁=20/2

х₁=10;                

х₂=(-b+√D)/2a

х₂=(30+10)/2

х₂=40/2

х₂=20;

Проверка путём подстановки  вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.