Прямоугольник 3100 состоит из 300 квадратов 11. Какое наибольшее число диагоналей можно провести в квадратах так, чтобы никакие две диагонали не имели общих концов? (В одном квадрате можно провести две диагонали, у них не будет общих концов. Общие внутренние точки разрешены.)
у = х + х³, y(-x) = (-x) + (-x)³ = -x - x³ = - (x + x³) - ф-ция нечетноя;
у = х² - 2, y(-x) = (-x)² - 2 = x² - 2 - четноя;
х^3 (-х)³ х³
у= ; у(-х) = = - - нечетная
х²+1 (-х)² + 1 х² + 1
1 1 1 1
у = х + ---, у(-х) = -х + = -х - = - (х + ) - нечетная
х -х х х
у = √1 - х²; у(-х ) = √1 - (-х)² = √1 - х² - четная
у = ³√х², у(-х) = ∛(-х)² = ∛х² - четная
Объяснение:
a = 1 (коэффициент при x^2)
b = 6 (коэффициент при x)
c = -5 (свободный элемент)
1) Вершина параболы находится по формуле
xв = -b/2a = -6/(2*1) = -3
yв находится подстановкой хв в исходное уравнение
ув = (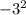
) + 6 *(-3) -5 = 9 -18 - 5 = -14
Координаты точки вершины (-3, -14)
2) Пересечение с ОХ происходит когда y = 0
D = 36 + 5*4 = 56
Тогда пересечение с осью ОХ происходит в точках:
x1 =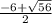
x2 =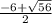
3) Пересечение с ОУ происходит когда x = 0
y = 0 + 0 -5 = -5
(0, -5)
4) x = m
y = 3
3 =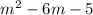
D = 36 + 32 = 68
m1 =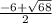
m2 =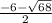
5)