У нас известно 2 члена арифметической прогрессии, составим из них систему и найдем и :
Выражаем ихз первого и получаем:
Подставляем во второе и получаем:
Подставляем d в выражение для и получаем:
Теперь напишем формулу для суммы n членов арифметической прогрессии:
теперь подставляем в это выражение найденные числа и получаем:
Получилась функция, которая зависит от n.
Нужно найти ее максимум:
Поскольку это парабола ветви которой направлены вниз (потому что перед стоит отрицательный коэффициент), то максимумом у нее будет точка, где производная принимает значение равное 0.
Найдем производную по n от этой функции:
Получим:
Теперь надо найти где она равно 0.
Решаем уравнение: получаем:
Теперь осталось выяснить какое n нам взять. n=28 или n=29.
Для этого надо просто вычислить значение суммы при n=28 и при n=29
Как мы видим S(29)>S(28),
значит при n=29 сумма принимает максимальное значение равное 1653
ответ: максимальное значение суммы первых n членов арифметической прогрессии равно 1653 и достигается при n=29
Х - скорость первого автомобиля. L - расстояние между пунктами. (Х+22) - скорость 2 автом. на втором участке. Тогда с учетом условия: L/Х - время движения 1 автомобиля 0,5L/33+0,5L/(Х+22) - время движения 2 астом. По условию они равны. L/Х =0,5L/33+0,5L/(Х+22) 1/Х=1/66+1/(2Х+44). Умножаем обе части на 66*Х*(Х+22) и избавляемся от знаменателя. Имеем: 66*(Х+22)=Х*(Х+22)+33*Х. Раскрываем скобки и переносим все в правую часть. Х^2+22Х+33Х-66Х-1452=0 (Х^2 - это Х в квадрате) Х^2-11Х-1452=0. Решаем квадратное уравнение Х1= 11/2+кор. квадр из [(11/2)^2+1452]=44 (км/час.) Х2=11/2-кор. квадр из [(11/2)^2+1452]<0 - не имеет смысла ответ: Х=44 км/час.
По свойству арифметической прогрессии:
У нас известно 2 члена арифметической прогрессии, составим из них систему и найдем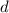 и
и 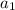 :
:
Выражаем ихз первого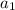 и получаем:
и получаем:
Подставляем во второе и получаем:
Подставляем d в выражение для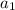 и получаем:
и получаем:
Теперь напишем формулу для суммы n членов арифметической прогрессии:
теперь подставляем в это выражение найденные числа и получаем:
Получилась функция, которая зависит от n.
Нужно найти ее максимум:
Поскольку это парабола ветви которой направлены вниз (потому что перед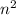 стоит отрицательный коэффициент), то максимумом у нее будет точка, где производная принимает значение равное 0.
стоит отрицательный коэффициент), то максимумом у нее будет точка, где производная принимает значение равное 0.
Найдем производную по n от этой функции:
Получим:
Теперь надо найти где она равно 0.
Решаем уравнение: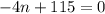 получаем:
получаем: 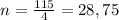
Теперь осталось выяснить какое n нам взять. n=28 или n=29.
Для этого надо просто вычислить значение суммы при n=28 и при n=29
Как мы видим S(29)>S(28),
значит при n=29 сумма принимает максимальное значение равное 1653
ответ: максимальное значение суммы первых n членов арифметической прогрессии равно 1653 и достигается при n=29
Х - скорость первого автомобиля.
L - расстояние между пунктами.
(Х+22) - скорость 2 автом. на втором участке.
Тогда с учетом условия:
L/Х - время движения 1 автомобиля
0,5L/33+0,5L/(Х+22) - время движения 2 астом.
По условию они равны.
L/Х =0,5L/33+0,5L/(Х+22)
1/Х=1/66+1/(2Х+44). Умножаем обе части на 66*Х*(Х+22) и избавляемся от знаменателя. Имеем:
66*(Х+22)=Х*(Х+22)+33*Х.
Раскрываем скобки и переносим все в правую часть.
Х^2+22Х+33Х-66Х-1452=0 (Х^2 - это Х в квадрате)
Х^2-11Х-1452=0. Решаем квадратное уравнение
Х1= 11/2+кор. квадр из [(11/2)^2+1452]=44 (км/час.)
Х2=11/2-кор. квадр из [(11/2)^2+1452]<0 - не имеет смысла
ответ: Х=44 км/час.