Любая сумма чисел этого числа будет ≤18, но при этом сумма чисел этого числа всегда будет больше нуля. Поскольку 0 не является натуральным числом в математике.
Теперь рассмотрим произведение двух чисел этого числа.
где:
a принимает значения — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
b принимает значения — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Заметим, что a ≠ 0, поскольку число не может начинаться с нуля.
Рассмотрим, если b = 0, то таких чисел:
То есть, вот эти числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
№1
находим корни числителя и знаменателя:
(x-3)^2 - всегда принимает неотрицательные значения. Значит при переходе через точку 3 неравенство знак не поменяет.
Используем метод интервалов:
точки (-2) и 5 - выколотые.
+ - + + - +
-------[-3]--------(-2)-------[3]--------(5)--------[8]---------->x
ответ:![x\in [-3;-2)\cup (5;8] \cup \{ 3 \}](/tpl/images/0999/4162/b28f6.png)
№2
точки (-1) и 4 - выколотые
+ + - +
------[-6]------(-1)------(4)------->x
ответ: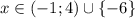
№3
замена:
получим:
обратная замена:
+ - + - +
-------[-√3]-------[-√2]--------[√2]-------[√3]-------->x
ответ:![x\in (-\infty;-\sqrt{3}]\cup [-\sqrt{2};\sqrt{2}]\cup [\sqrt{3};+\infty)](/tpl/images/0999/4162/cc812.png)
90 чисел.
Объяснение:
Нам подходят все натуральные числа ≤ 100.
Рассмотрим сумму двух чисел.
Заметим, что 0 нацело делится на 100.
Любая сумма чисел этого числа будет ≤18, но при этом сумма чисел этого числа всегда будет больше нуля. Поскольку 0 не является натуральным числом в математике.
Теперь рассмотрим произведение двух чисел этого числа.
где:
a принимает значения — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
b принимает значения — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Заметим, что a ≠ 0, поскольку число не может начинаться с нуля.
Рассмотрим, если b = 0, то таких чисел:
То есть, вот эти числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Всего, подходящих нам чисел: 100 - 10 = 90 чисел.