Для начала приведем к общему знаемнателю. Общий знаменатель 6х(6+х)
Теперь будем находить ОДЗ(область допустим значений, тоже самое, что и область определения). Известно, что знаменатель дроби не может быть равен 0, поэтому
6x=0 6+x=0
x=0 x=-6
Значит х не может быть равен 0 и -6. Поэтому ОДЗ
б) y=√x -√(x-4)
Мы знаем, что подкоренное выражение всегда неотрицательно, поэтому ОДЗ этой функции будет являться система неравенств
a)y=1/6x +1/(6+x)
Для начала приведем к общему знаемнателю. Общий знаменатель 6х(6+х)
Теперь будем находить ОДЗ(область допустим значений, тоже самое, что и область определения). Известно, что знаменатель дроби не может быть равен 0, поэтому
6x=0 6+x=0
x=0 x=-6
Значит х не может быть равен 0 и -6. Поэтому ОДЗ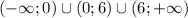
б) y=√x -√(x-4)
Мы знаем, что подкоренное выражение всегда неотрицательно, поэтому ОДЗ этой функции будет являться система неравенств
Решением системы будет являться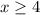
в)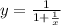
Знаменатель не может быть равен 0, поэтому
Значит х не равняется 0 и -1, а ОДЗ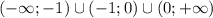
Чтобы это сделать, нужно доказать, что: F'(x) = f(x)
Найдем F'(x):
F'(x) = -3/8 * (cos4x/3)' + 3/4*(cos2x/3)'
(cos4x/3)' = -sin4x/3 * (4x/3)' = -4/3sin4x/3
(cos2x/3)' = -sin2x/3 * (2x/3)' = -2/3sin2x/3
F'(x) = -3/8 * (-4/3sin4x/3) + 3/4*(-2/3sin2x/3)
F'(x) = 1/2*sin4x/3 - 1/2sin2x/3
Пусть 4х/3 = y
F'(x) = 1/2sin(2y) - 1/2siny
F'(x) = 1/2*(sin(2y) - siny)
F'(x) = 1/2* (2siny*cosy - siny)
F'(x) = siny*cosy - 1/2siny
Вернемся к замене
siny = sin4x/3 = sinx/3 - по формуле приведения
cos4x/3 = cosx/3 - по формуле приведения
Возможно где-то ошибся,но тип решения такой, и должно получится,что F'(x) = sinx/3*cosx
Тогда будет доказано,что это первообразная