1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если , а , при k>5
То есть, , при k>5, то по закону транзитивности:
, при k>5 - ч.т.д
I автомобиль:
Скорость х км/ч
Время на весь путь (1/х) ч.
II автомобиль :
I-я половина пути 1 : 2 = 1/2 = 0,5
Скорость (х-11) км/ч
Время на этот путь 0,5/(х-11) часов
II-я половина пути 0,5
Скорость 66 км/ч
Время на этот путь 0,5/66 часов.
Зная, что автомобили прибыли одновременно, составим уравнение:
1/х = 0,5/(х-11) + 0,5/66
1/x - 0.5/(x-11) = 0.5/66
знаменатели дробей не должны быть равны 0 :
х ≠0 ; х≠ 11
(x - 11 - 0.5x) / x(x-11) = 0.5/66
(0.5x-11)/ (x² - 11x) = 0.5/66
0.5(x² - 11x) = 66(0.5x-11) |*2
x² -11x = 2*66*0.5x - 2*66*11
x² -11x = 66x - 1452
x² - 11x -66x + 1452=0
x² - 77x +1452 =0
D = (-77)² - 4*1 * 1452 = 5929 - 5808 = 121 = 11²
D>0 - два корня уравнения
х₁ = ( - (-77) - 11)/(2 *1) = (77-11)/2 = 66/2 = 33 не удовлетворяет условию задачи (<42 км/ч)
х₂ = (77+11)/2 = 88/2 = 44 (км/ч) скорость I автомобиля
ответ: 44 км/ч скорость I автомобиля.
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если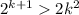 , а
, а 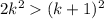 , при k>5
, при k>5
То есть,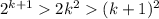 , при k>5, то по закону транзитивности:
, при k>5, то по закону транзитивности: