2) Если функция задана формулой f(x) = ax²+bx+c, то сначала нужно найти координаты вершины. Сначала координату х : . Затем ее подставить в формулу и найти координату у₀=f(x₀)=ax₀²+bx₀+c.
Если a>0, то область значений функции E(f)=[y₀;+∞).
Если а<0, то область значений функции E(f)=(-∞;y₀].
Разложим каждую дробь на множители:
1). (а³ +8) / (3а-6) = (а³ +2³) / (3(а-2)) = (а+2)(а²-2а+4) / (3(а-2))
а²-2а+4 = 0
Д=4-16=-12 <0 - не раскладывается на множители, оставляем как есть
2). (а²+4а+4)/(а²-2а)
а²+4а+4=0
Д=16-16=0 - 1 корень
а=-4/2=-2
а²+4а+4 = (а+2)²
(а²+4а+4)/(а²-2а) = (а+2)² / (а(а-2))
3). (а²-2а+4) / (а²-4) = (а²-2а+4) / ((а-2)(а+2))
выполним деление дробей:
(а+2)(а²-2а+4) / (3(а-2)) : (а+2)² / (а(а-2)) : (а²-2а+4) / ((а-2)(а+2)) = (а+2)(а²-2а+4) / (3(а-2)) * (а(а-2)) / (а+2)² * ((а-2)(а+2))/(а²-2а+4) = (после всех сокращений) = (а(а-2))/3 = (а²-2а)/3
1) Если функция f(x) задана графиком, то нужно найти на графике координату у₀ вершины параболы.
Если ветви параболы направлены вниз, то область значений E(f)=(-∞;y₀].
Если ветви параболы направлены вверх, то область значений E(f)=[y₀;+∞).
------------------------------------------------------------------------
2) Если функция задана формулой f(x) = ax²+bx+c, то сначала нужно найти координаты вершины. Сначала координату х :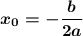
. Затем ее подставить в формулу и найти координату у₀=f(x₀)=ax₀²+bx₀+c.
Если a>0, то область значений функции E(f)=[y₀;+∞).
Если а<0, то область значений функции E(f)=(-∞;y₀].
----------------------------------------------------------------------------------
3) Если функция задана формулой вида f(x) = a(x - x₀)² + у₀, то координаты вершины параболы присутствуют в явном виде (x₀; y₀).
Если a>0, то область значений функции E(f)=[y₀;+∞).
Если а<0, то область значений функции E(f)=(-∞;y₀].