Итак, для решения примера надо каждое число представить в степени какого-то числа, желательно чтобы было число одно и то же. Объясняю, к примеру, надо представить число 512 как какое-то число в какой-то степени. 512 это у нас 2 в степени 9 (). Итак, сейчас наша задача представить каждое число как число 2 в какой-то степени. По порядку: 512=, 128=, 256=, 64=, 4=, 16=, 8=. С этим мы справились, а сейчас нужно каждое число умножить на их степени, в которых они стоят. Сейчас покажу, как это всё выглядит на данном этапе:
Далее всё просто. Чтобы возвести число, стоящее в степени, в степень, то нужно показатели степеней перемножить:
Ну а дальше простая математика 2 класса: при умножении чисел с одинаковыми основаниями, но с разными степенями, их степени складываются; при делении - степени вычитаются. Подсчитаем результат в числителе:
sin2x cosx = cos2x sinx
2sinxcosxcosx=cos2xsinx sinx=0 x=Пk
2cos^2x=cos2x
2cos^2x=2cos^2x-1 ∅
ответ x=Пk
cos5x cosx = cos4x
cos4x+cos6x=2cos4x
cos6x-cos4x=0
-2sin5xsinx=0
x=Пk
x=Пk/5
3+sin2x = 4sin^2x
3sin^2x+3cos^2x+2sinxcosx=4sin^2x
sin^2x-3cos^2x-2sinxcosx=0
sinx/cosx-3cosx/sinx-2=0
tgx-3/tgx-2=0
tg^2x-2tgx-3=0 tgx=3 tgx=-1
x=-П/4+Пk
x=arctg3+Пk
cos2x + cos^2x + sinx cos x = 0
2cos^2x-sin^2x+sinxcosx=0 |sinxcosx
2cosx/sinx-sinx/cosx+1=0
2ctgx-tgx+1=0
2/tgx-tgx+1=0
-tg^2x+tgx+2=0 tg^2x-tgx-2=0
tgx=(1+-3)/2 tgx=2 tgx=-1
x=-П/4+Пk
x=arctg2+Пk
3 cos 2x + sin^2x + 5 sinx cosx = 0
3cos^2x-2sin^2x+5sinxcosx=0
3cosx/sinx-2sinx/cosx+5=0
3/tgx-2tgx+5=0
2tgx-3/tgx-5=0
2tg^2x-5tgx-3=0
tgx=(5+-7)/4 tgx=3 tgx=-1/2
x=arctg3+Пk
x=-arctg1/2+Пk
Итак, для решения примера надо каждое число представить в степени какого-то числа, желательно чтобы было число одно и то же. Объясняю, к примеру, надо представить число 512 как какое-то число в какой-то степени. 512 это у нас 2 в степени 9 (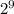 ). Итак, сейчас наша задача представить каждое число как число 2 в какой-то степени. По порядку: 512=
). Итак, сейчас наша задача представить каждое число как число 2 в какой-то степени. По порядку: 512=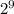 , 128=
, 128=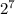 , 256=
, 256=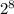 , 64=
, 64=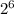 , 4=
, 4=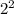 , 16=
, 16=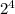 , 8=
, 8=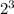 . С этим мы справились, а сейчас нужно каждое число умножить на их степени, в которых они стоят. Сейчас покажу, как это всё выглядит на данном этапе:
. С этим мы справились, а сейчас нужно каждое число умножить на их степени, в которых они стоят. Сейчас покажу, как это всё выглядит на данном этапе:
Далее всё просто. Чтобы возвести число, стоящее в степени, в степень, то нужно показатели степеней перемножить:
Ну а дальше простая математика 2 класса: при умножении чисел с одинаковыми основаниями, но с разными степенями, их степени складываются; при делении - степени вычитаются. Подсчитаем результат в числителе:
В знаменателе:
И последнее действие:
ответ: 2^{-33}