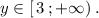1) Строим параболу y=x² . Она прохy=3+2x² y=2x² y=x²одит через точки (0,0) - вершина , (-1, 1) , (1,1) .
2) Затем эту параболу растягиваем в 2 раза вдоль оси ординат (с коэффициентом k=2), и получаем параболу y=2x² . Она проходит через точки (0,0) - вершина , (-1,2) , (1,2) .
3) Теперь поднимаем параболу y=2x² на 3 единицы вверх вдоль рси ОУ, получаем параболу y=3+2x² . Её вершина в точке (0,3) . Проходит через точки (-1,5) , (1,5) .
4) Область определения заданной функции , а область значений
-√х=-х+12|• (-1)
√х= х-12
Подносим всё к квадрату
х= (х-12)^2
х= х^2-24х+144
х-х^2+24х-144=0
25х-х^2-144=0
-х^2+25х-144=0 |• (-1)
х^2-25х+144=0
D = 625 - 4•144= 625-576= 49=7
x1= (25+7):2= 16
x2=(25-7):2=9
Проверим:
9-√9-12= -6
9- сторонній корінь
Відповідь: х=16
2) 5хх^4•3х^2-2=0
15х^7-2=0
15х^7=2 | :15
х^7= 2/15
х= (7√2•15^6):15
( це корінь в 7 степені ,2•15^6 повністю під коренем)
3) (2х^2+3)^2-12(2х^2+3)+11=0
4х^4-12х^2+9- 24^2-36+11=0
Заміна: х^2=а
4а^2-36а - 16=0 | :4
а^2-9а-4=0
D= 81+ 4•4= 97=√97 ≈9,8
x1= (9+9,8):2= 9,4
x2= (9-9,8):2= -0,4
x^2= 9,5
x^2= - 0,4
x=≈3,1; -3,1
x= ≈0,63; -0,63
Проверь правильно ли переписано условие, ибо 2 последних примера выходят странно.
1) Строим параболу y=x² . Она прохy=3+2x² y=2x² y=x²одит через точки (0,0) - вершина , (-1, 1) , (1,1) .
2) Затем эту параболу растягиваем в 2 раза вдоль оси ординат (с коэффициентом k=2), и получаем параболу y=2x² . Она проходит через точки (0,0) - вершина , (-1,2) , (1,2) .
3) Теперь поднимаем параболу y=2x² на 3 единицы вверх вдоль рси ОУ, получаем параболу y=3+2x² . Её вершина в точке (0,3) . Проходит через точки (-1,5) , (1,5) .
4) Область определения заданной функции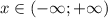
, а область значений 