(-∞; (15 - √253) / 14) ∪ ((15 + √253) / 14; +∞)
Объяснение:
(3 - х)(7х + 1) < 5х + 2
21х + 3 - 7х² - х < 5x + 2
-7x² + 20x + 3 < 5x + 2
-7x² + 20x - 5x + 3 - 2 < 0
-7x² + 15x + 1 = 0
D = 15² - 4 * (-7) = 225 + 28 = 253
√D = √253
x₁ = (-15 - √253) / (-7 * 2) = -(15 + √253) / (-14) = (15 + √253)/14 (примерно 2,207)
x₂ = (-15 + √253) / (-7 * 2) = -(15 - √253) / (-14) = (15 - √253) / 14 (примерно -0,06)
начертим координатную прямую (см. рис)
подставим -1 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - (-1)) * (7 * (-1) + 1) - 5 * (-1) - 2 =
= 4 * (-7 + 1) + 5 - 2 =
= -6 * 4 + 5 - 2 =
= -24 + 5 - 2 = -21
впишем в промежутке от -∞ до (15 - √253) / 14 знак "-"
подставим 0 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - 0) * (7 * 0 + 1) - 5 * 0 - 2 = 3 * 1 - 2 = 1
впишем в промежутке от (15 - √253) / 14 до (15 + √253)/14 знак "+"
подставим 3 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - 3) * (7 * 3 + 1) - 5 * 3 - 2 = 0 - 15 - 2 = -17
впишем в промежутке от (15 + √253) / 14 до +∞ знак "-"
Неравенство принимает отрицательное значение в промежутках:
№1
находим корни числителя и знаменателя:
(x-3)^2 - всегда принимает неотрицательные значения. Значит при переходе через точку 3 неравенство знак не поменяет.
Используем метод интервалов:
точки (-2) и 5 - выколотые.
+ - + + - +
-------[-3]--------(-2)-------[3]--------(5)--------[8]---------->x
ответ:
№2
точки (-1) и 4 - выколотые
+ + - +
------[-6]------(-1)------(4)------->x
№3
замена:
получим:
обратная замена:
+ - + - +
-------[-√3]-------[-√2]--------[√2]-------[√3]-------->x
(-∞; (15 - √253) / 14) ∪ ((15 + √253) / 14; +∞)
Объяснение:
(3 - х)(7х + 1) < 5х + 2
21х + 3 - 7х² - х < 5x + 2
-7x² + 20x + 3 < 5x + 2
-7x² + 20x - 5x + 3 - 2 < 0
-7x² + 15x + 1 = 0
D = 15² - 4 * (-7) = 225 + 28 = 253
√D = √253
x₁ = (-15 - √253) / (-7 * 2) = -(15 + √253) / (-14) = (15 + √253)/14 (примерно 2,207)
x₂ = (-15 + √253) / (-7 * 2) = -(15 - √253) / (-14) = (15 - √253) / 14 (примерно -0,06)
начертим координатную прямую (см. рис)
подставим -1 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - (-1)) * (7 * (-1) + 1) - 5 * (-1) - 2 =
= 4 * (-7 + 1) + 5 - 2 =
= -6 * 4 + 5 - 2 =
= -24 + 5 - 2 = -21
впишем в промежутке от -∞ до (15 - √253) / 14 знак "-"
подставим 0 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - 0) * (7 * 0 + 1) - 5 * 0 - 2 = 3 * 1 - 2 = 1
впишем в промежутке от (15 - √253) / 14 до (15 + √253)/14 знак "+"
подставим 3 вместо х в неравенство (3 - х)(7х + 1) - 5х - 2 < 0 . Будет:
(3 - 3) * (7 * 3 + 1) - 5 * 3 - 2 = 0 - 15 - 2 = -17
впишем в промежутке от (15 + √253) / 14 до +∞ знак "-"
Неравенство принимает отрицательное значение в промежутках:
(-∞; (15 - √253) / 14) ∪ ((15 + √253) / 14; +∞)
№1
находим корни числителя и знаменателя:
(x-3)^2 - всегда принимает неотрицательные значения. Значит при переходе через точку 3 неравенство знак не поменяет.
Используем метод интервалов:
точки (-2) и 5 - выколотые.
+ - + + - +
-------[-3]--------(-2)-------[3]--------(5)--------[8]---------->x
ответ:![x\in [-3;-2)\cup (5;8] \cup \{ 3 \}](/tpl/images/0999/4162/b28f6.png)
№2
точки (-1) и 4 - выколотые
+ + - +
------[-6]------(-1)------(4)------->x
ответ: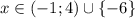
№3
замена:
получим:
обратная замена:
+ - + - +
-------[-√3]-------[-√2]--------[√2]-------[√3]-------->x
ответ:![x\in (-\infty;-\sqrt{3}]\cup [-\sqrt{2};\sqrt{2}]\cup [\sqrt{3};+\infty)](/tpl/images/0999/4162/cc812.png)