Реши задачу и запиши ответ Высота ВН, опущенная на гипотенузу АС = 26 прямоугольного треугольника АВС, делит гипотенузу на отрезки А.Н и НС, причем АН : = 4 : 9. Найди длину меньшего катета треугольника. ответ:

2 см и 2 см

Объяснение:

Дан прямоугольник, периметр которого равен 8 см. Тогда сумма двух сторон равна 8:2 = 4 см. Обозначим через x одну сторону прямоугольника. Тогда вторая сторона равна: 4–x. Теперь составим функцию площади прямоугольника: y=x·(4–x)=4·x-x². Дифференцируем функцию

y'=(4·x–x²)'=4–2·x.

Находим критические точки функции:

y'=0 ⇔ 4–2·x=0 ⇔ x=2 – критическая точка.  

Проверим знаки производной:

при x<2: y'=4–2·x>0 и при x>2: y'=4–2·x<0.

Значит, x=2 точка максимума. Тогда

yмакс=y(2)=4·2–2²=8–4=4 см²,

а стороны x=2 см и 4–2=2 см.

ответ: Минимум (-3;-1). Рост функции на интервале (-3;+∞). Функция убывает на промежутке (-∞;-3)

Объяснение:

Наименьшее значение:

Перед нами уравнение параболы. Известно, что экстремальное значение параболы достигается при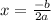 (здесь b - коэффициент при x, а а -  коэффициент при x^2)

Находим x:

x = -3 ⇒ подставляем это значение в функцию ⇒ y = -1 (данный y - минимум, которого может достичь функция)

Точка минимума - (-3;-1)

Промежуток, на котором функция возрастает:

Понятно, что данная парабола ветвями вверх, так как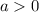 . Значит, функция возрастает после прохождения своего минимума:

Рост функции:

x ∈ (-3; +∞)

Промежуток на котором функция убывает:

Функция убывает пока не достигнет своего минимума

Уменьшение функции:

x ∈ (-∞; -3)