Объяснение:
4)
√(x²-3x+11)-4x²+12x=11
√(x²-3x+11)-4x²+12x-44=11-44
√(x²-3x+11)-4*(x²-3x+11)=-33
Пусть √(x²-3x+11)=t≥0 ⇒
t-4t²=-33
4t²-t-33=0 D=529 √D=23
t₁=-2,75 ∉
t²=3 ⇒
√(x²-3x+11)=3
(√(x²-3x+11))²=3²
x²-3x+11=9
x²-3x+2=0 D=1
x₁=2 x₂=1.
5)
ОДЗ: x-1≠0 x≠1 2-x≠0 x≠2.
Пусть ⇒
t₁=7 t₂=-1 ∉ ⇒
Объяснение:
4)
√(x²-3x+11)-4x²+12x=11
√(x²-3x+11)-4x²+12x-44=11-44
√(x²-3x+11)-4*(x²-3x+11)=-33
Пусть √(x²-3x+11)=t≥0 ⇒
t-4t²=-33
4t²-t-33=0 D=529 √D=23
t₁=-2,75 ∉
t²=3 ⇒
√(x²-3x+11)=3
(√(x²-3x+11))²=3²
x²-3x+11=9
x²-3x+2=0 D=1
x₁=2 x₂=1.
5)
Пусть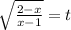 ⇒
⇒
t₁=7 t₂=-1 ∉ ⇒