В решении.
Объяснение:
3. Функция здана уравнением у= -2x² + 3x + 5;
а) В какой точке график данной функции пересекает ось Oу?
Любой график пересекает ось Оу при х=0:
у = -2 * 0² + 3 * 0 + 5 = 5;
Координаты точки пересечения графиком оси Оу: (0; 5);
б) Найдите точки пересечения графика функции с осью Oх.
Любой график пересекает ось Ох при у=0:
-2x² + 3x + 5 = 0/-1
2х² - 3х - 5 = 0
D=b²-4ac = 9 + 40 = 49 √D=7
х₁=(-b-√D)/2a
х₁=(3-7)/4
х₁= -4/4
х₁= -1;
х₂=(-b+√D)/2a
х₂=(3+7)/4
х₂=10/4
х₂= 2,5;
Координаты точек пересечения графиком оси Ох: (-1; 0); (2,5; 0);
в) Запишите уравнение оси симметрии графика данной
функции.
Ось симметрии равна х₀;
Формула: x₀ = -b/2a;
у= -2x² + 3x + 5;
x₀ = -3/-4
x₀ = 0,75;
Ось симметрии Х = 0,75;
г) постройте график:
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= -1 и х= 2,5.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -2x² + 3x + 5;
Таблица:
х -2 -1 0 1 2 3
у -9 0 5 6 3 -4
По вычисленным точкам построить параболу.
Функция
- убывает на
- возрастает на
Точка минимума функции:
x = -0.2
Функция определена на R, или
Для нахождения промежутков возрастания (убывание) и точек экстремума находим производную функции f'(x):
Производная исследуемой функции также определена на R, или
Найдем критические точки
Т.к. производная исследуемой функции также определена на R, или , найдем нули производной :
что равносильно совокупности:
Найдем промежутки возрастания / убывания:
Функция возрастает при f'(x) > 0
убывает при f'(x) < 0
Для этого исследуем точку x = -0,2 на экстремум: знак производной
- при х < -0.2 f'(x) < 0 => функция f(x)
убывает на
- при х > -0.2 f'(x) < 0 => функция f(x)
возрастает на
В точке x = -0.2 происходит смена функции
с убывания --> на возрастание
Следовательно, x = -0.2 - является единственной точкой экстремума, а именно это - точка минимума функции
В решении.
Объяснение:
3. Функция здана уравнением у= -2x² + 3x + 5;
а) В какой точке график данной функции пересекает ось Oу?
Любой график пересекает ось Оу при х=0:
у = -2 * 0² + 3 * 0 + 5 = 5;
Координаты точки пересечения графиком оси Оу: (0; 5);
б) Найдите точки пересечения графика функции с осью Oх.
Любой график пересекает ось Ох при у=0:
-2x² + 3x + 5 = 0/-1
2х² - 3х - 5 = 0
D=b²-4ac = 9 + 40 = 49 √D=7
х₁=(-b-√D)/2a
х₁=(3-7)/4
х₁= -4/4
х₁= -1;
х₂=(-b+√D)/2a
х₂=(3+7)/4
х₂=10/4
х₂= 2,5;
Координаты точек пересечения графиком оси Ох: (-1; 0); (2,5; 0);
в) Запишите уравнение оси симметрии графика данной
функции.
Ось симметрии равна х₀;
Формула: x₀ = -b/2a;
у= -2x² + 3x + 5;
x₀ = -3/-4
x₀ = 0,75;
Ось симметрии Х = 0,75;
г) постройте график:
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= -1 и х= 2,5.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -2x² + 3x + 5;
Таблица:
х -2 -1 0 1 2 3
у -9 0 5 6 3 -4
По вычисленным точкам построить параболу.
Функция
- убывает на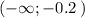
- возрастает на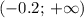
Точка минимума функции:
x = -0.2
Объяснение:
Функция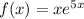
определена на R, или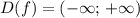 
Для нахождения промежутков возрастания (убывание) и точек экстремума находим производную функции f'(x):
Производная исследуемой функции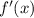
также определена на R, или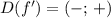 
Найдем критические точки
Т.к. производная исследуемой функции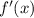
также определена на R, или 
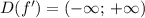, найдем нули производной :
что равносильно совокупности:
Найдем промежутки возрастания / убывания:
Функция возрастает при f'(x) > 0
убывает при f'(x) < 0
Для этого исследуем точку x = -0,2 на экстремум: знак производной
- при х < -0.2 f'(x) < 0 => функция f(x)
убывает на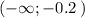
- при х > -0.2 f'(x) < 0 => функция f(x)
возрастает на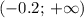
В точке x = -0.2 происходит смена функции
с убывания --> на возрастание
Следовательно, x = -0.2 - является единственной точкой экстремума, а именно это - точка минимума функции