а) поиск наибольшего значения сводится к поиску точки экстремума. Надём производную и, приравняв её нулю, найдём x:
В точке x=1 производная меняет свой знак с + на -, значит в этой точке находится экстремум максимум y(1)=-6.
б) при x>1 производная отрицательна, значит функция на этом промежутке убывает;
в) при x<1 производная положительна, значит функция на этом промежутке возрастает.
2. см. влож.
3,4. x^2 - первая функция (зелёная парабола), -x^2 +2x-7 - вторая функция (красная парабола). Ветви первой направлены вверх, ветви второй вниз. Вершина первой в точке (0;0), вершина второй смещена вправо и вниз (в червёртую четверть). Первая симметрична относительно оси ординат, вторая нет.
2)7 * 5 (в степени х) - 5 (в степени х+2) = - 450
7 * 5 (в степени х) - 5 (в степени х) * 25 = - 450
5 (в степени х) * ( 7- 25 ) = - 450
5 (в степени х) * (-18) = - 450
5 (в степени х) = 25
5 (в степени х) = 5 (в степени 2)
x=2
ответ:2
3) 2 * 9 (в степени х) - 3 (в степени х+1) - 9 =0
2 * 3 (в степени 2х) - 3 (в степени х) * 3 - 9 =0
Пусть 3 (в степени х) = t, тогда t(в степени 2) = 3 (в степени 2х)
2 * t(в степени 2) - 3 t - 9 =0
D=81, t1=3, t2=-1.5
Вернемся к исходной переменной
3 (в степени х) = 3 и 3 (в степени х)= -1.5
x=1 3 (в степени х)>0(должно быть), значит нет корня
ответ:1
1.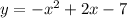
а) поиск наибольшего значения сводится к поиску точки экстремума. Надём производную и, приравняв её нулю, найдём x:
В точке x=1 производная меняет свой знак с + на -, значит в этой точке находится экстремум максимум y(1)=-6.
б) при x>1 производная отрицательна, значит функция на этом промежутке убывает;
в) при x<1 производная положительна, значит функция на этом промежутке возрастает.
2. см. влож.
3,4. x^2 - первая функция (зелёная парабола), -x^2 +2x-7 - вторая функция (красная парабола). Ветви первой направлены вверх, ветви второй вниз. Вершина первой в точке (0;0), вершина второй смещена вправо и вниз (в червёртую четверть). Первая симметрична относительно оси ординат, вторая нет.