РЕШИТЬ: Какие из функций: y=x7−9; y=−9x3+7; y=22⋅|7+x|−9; y=7; y=−9x+37; y=22x+710; y=7x являются линейными.
2.Какие из функций:y=14x−9; y=14x+21; y=19⋅|−9+x|+14; y=−9x; y=14x3−9; y=−9x2+14; y=x9+14 являются линейными.
3.Линейная функция задана формулой: y=2x−3
Найдите значение функции, если значение аргумента равно: -5.
4.Линейная функция задана формулой: y=−13x−8
Найдите значение функции, если значение аргумента равно: 5.

Объяснение:

x²-3x<0

x(x-3)<0

Допустим:

x₁=0; x-3=0; x₂=3

Проверка при x₁>0 и x₂>3: 4²-3·4<0; 16-12<0; 4>0 - неравенство не соблюдается.

Проверка при x₁<0 и x₂<3: (-1)²-3·(-1)<0; 1+3<0; 4>0 - неравенство не соблюдается.

Проверка при x₁>0 и x₂<3: 1²-3·1<0; 1-3<0; -2<0 - неравенство соблюдается.

Следовательно, 0<x<3⇒x∈(0; 3).

              /\

0/\3x

x²-7x-30≥0

Допустим:

x²-7x-30=0; D=49+120=169

x₁=(7-13)/2=-6/2=-3

x₂=(7+13)/2=20/2=10

Проверка при x₂>10: 11²-7·11-30≥0; 121-77-30≥0; 14>0 - неравенство соблюдается; при x₁>-3: 0²-7·0-30≥0; -30<0 - неравенство не соблюдается.

Проверка при x₁<-3: (-4)²-7·(-4)-30≥0; 16+28-30≥0; 14>0 - неравенство соблюдается.

Следовательно, -3>x>10⇒x∈(-∞; -3]∪[10; +∞).

\                               /

\-310/x

1)

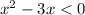
Если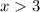 , обе скобки дают положительный результат - такие иксы нам не подходят

Если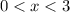 , первая скобка даёт положительный результат, а вторая отрицательный - такие иксы подходят

Если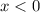 , обе скобки дают отрицательный результат - такие иксы тоже не подходят (минус на минус - плюс)

Если или , произведение даёт ноль - не подходит

ответ: x∈(0;3)

2)

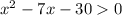
Если , обе скобки дают положительный результат - такие иксы нам подходят

Если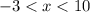 , первая скобка даёт отрицательный результат, а вторая положительный - такие иксы не подходят

Если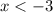 , обе скобки дают отрицательный результат - такие иксы тоже подходят (минус на минус - плюс)

Если или 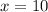, произведение даёт ноль - не подходит

ответ: x∈(-∞;-3)∪(10;∞)

Если остались вопросы - в комментарии. Буду благодарен, если отметишь моё решение как "Лучший ответ"