Метод интервалов – простой решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной. Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
1. Уравнение можно решить так же, как это сделал(а) Agnesmile02464, но можно ещё сделать через дискриминант.
x^2 - 6x - 7 = 0
D = b^2 - 4ac;
D = -6^2 - 4 * 1 * (-7) = 36 + 28 = 64
x = (-b +- )/2a
x1 = (6 + )/2 * 1 = (6 + 8)/2 = 14/2 = 7
x2 = (6 - )/2 * 1 = (6 - 8)/2 = -2/2 = -1
2. Для решения этого задания есть специальная формула, но я её благополучно забыл.) Попробую решить через систему. Для решения этого задания нам понадобится всеми любимая формула y=kx + b. Нужно взять две любые точки, через которые проходит прямая, и подставить. Получаем:
(-1;3) и (1;-3)
Подставляем в формулу, получаем систему:
{3 = -k + b
{-3 = k + b
Перенесем значения, чтобы были легче:
{k - b = -3
{-k - b = 3
Нам нужно найти k и b. Отнимем эти уравнения, чтобы избавиться от b и, для начала, найти k:
k - b - (-k) - (-b) = -3 - 3
k - b + k + b = -6
2k = -6
k = -3
Подставим в саааамое первое уравнение:
3 = - (-3) + b
3 = 3 + b
-b = 3 - 3
b = 0
k = -3, b = 0. Подставляем значения в y = kx + b и получаем функцию:
y = -3x
ответ 1)
Объяснение: Если что-то непонятно - не стесняйся и спрашивай ;)
Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
1. Уравнение можно решить так же, как это сделал(а) Agnesmile02464, но можно ещё сделать через дискриминант.
x^2 - 6x - 7 = 0
D = b^2 - 4ac;
D = -6^2 - 4 * 1 * (-7) = 36 + 28 = 64
x = (-b +-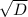
)/2a
x1 = (6 +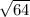
)/2 * 1 = (6 + 8)/2 = 14/2 = 7
x2 = (6 -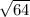
)/2 * 1 = (6 - 8)/2 = -2/2 = -1
2. Для решения этого задания есть специальная формула, но я её благополучно забыл.) Попробую решить через систему. Для решения этого задания нам понадобится всеми любимая формула y=kx + b. Нужно взять две любые точки, через которые проходит прямая, и подставить. Получаем:
(-1;3) и (1;-3)
Подставляем в формулу, получаем систему:
{3 = -k + b
{-3 = k + b
Перенесем значения, чтобы были легче:
{k - b = -3
{-k - b = 3
Нам нужно найти k и b. Отнимем эти уравнения, чтобы избавиться от b и, для начала, найти k:
k - b - (-k) - (-b) = -3 - 3
k - b + k + b = -6
2k = -6
k = -3
Подставим в саааамое первое уравнение:
3 = - (-3) + b
3 = 3 + b
-b = 3 - 3
b = 0
k = -3, b = 0. Подставляем значения в y = kx + b и получаем функцию:
y = -3x
ответ 1)
Объяснение: Если что-то непонятно - не стесняйся и спрашивай ;)