Решить неравенства:
sin2x ≤ - (√3)/2
cosx > (√2)/2
sinx(x-π/3) > (√3)/2
cos(2x+π/4) < - (√2)/2

cos(3x+3y) = cos((2x+y) + (2y+x)) = cos(2x+y)*cos(2y+x) - sin(2x+y)*sin(2y+x)

Обозначим 2x+y = a; 2y+x = b.

Нам надо найти:

cos a*cos b - sin a*sin b

Нам известно:

{ cos a - cos b = 1/2

{ sin a - sin b = 1

Возводим в квадрат оба уравнения

{ (cos a - cos b)^2 = cos^2 a - 2cos a*cos b + cos^2 b = 1/4

{ (sin a - sin b)^2 = sin^2 a - 2sin a*sin b + sin^2 b = 1

Складываем уравнения

cos^2 a + sin^2 a - 2(cos a*cos b + sin a*sin b) + cos^2 b + sin^2 a = 5/4

1 - 2cos(a-b) + 1 = 5/4

cos(a-b) = 2 - 5/4 = 3/4

ответ: 3/4

. Будем считать, что

1-й случай.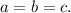  Разделив уравнение на 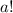, получаем 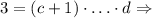в правой части на самом деле один множитель; 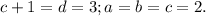Проверка: 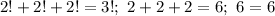- верно. Итак, одно решение найдено.

2-й случай.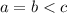 . Разделив уравнение на 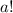, получаем 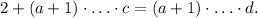Следовательно, 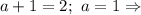уравнение имеет вид 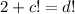Но два факториала не могут отличаться на 2, поэтому в этом случае уравнение решений не имеет.

3-й случай.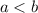 .  Разделив уравнение на 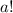, получаем 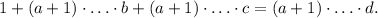Такое уравнение не может иметь решений, так как все слагаемые, кроме первого, делятся на a+1.

ответ: a=b=c=2; d=3