1) Квадратичная функция y=x^2 ; график функции парабола, ветви направлены вверх, с центром в О (0;0), проходит через точки: (1;1) и (-1;1), (2; 4) и (-2;4), (0; 1.5) и (-2; 1.5)
Линейная функция y=2x+3 ; график функции прямая, проходящая через точки (0;3) и (2;7)
По заданным точкам строим 2 графика.
2) Для нахождения точек пересечения приравняем y=y и найдем точки на абциссе (х):
2x+3=x^2;
x^2-2x-3=0
а=1
b=-2
c=-3
D= 4+12 = 16, х>0, х1,х2, =4
х1= (-b+4)/2a= 3
х2= (-b-4)/2a= -1
Подставим найденные x в уравнение y=x^2 и найдем ординату (у), y1=9; y2=1. Так точки пересечения двух графиков: (3;9) и (-1; 1).
Объяснение:
y = sinx .
a) D( sin ) = R ;
b) E( sin ) = [ - 1 ; 1 ] ;
c) T = 2π ; - найменший додатний період функції y = sinx ;
d) проміжки зростання [ - π/2 + 2πn ; π/2 + 2πn ] , nЄ Z ;
проміжки спадання [ π/2 + 2πn ; 3π/2 + 2πn ] , nЄ Z .
e) sinx > 0 при хЄ ( 2πn ; π + 2πn ) , nЄ Z ;
sinx < 0 при хЄ ( π + 2πn ; 2π + 2πn ) , nЄ Z .
f ) sin( - x ) = - sinx , тому функція y = sinx - непарна . Її графік
симетричний відносно початку координат .
1) Квадратичная функция y=x^2 ; график функции парабола, ветви направлены вверх, с центром в О (0;0), проходит через точки: (1;1) и (-1;1), (2; 4) и (-2;4), (0; 1.5) и (-2; 1.5)
Линейная функция y=2x+3 ; график функции прямая, проходящая через точки (0;3) и (2;7)
По заданным точкам строим 2 графика.
2) Для нахождения точек пересечения приравняем y=y и найдем точки на абциссе (х):
2x+3=x^2;
x^2-2x-3=0
а=1
b=-2
c=-3
D= 4+12 = 16, х>0, х1,х2,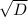 =4
=4
х1= (-b+4)/2a= 3
х2= (-b-4)/2a= -1
Подставим найденные x в уравнение y=x^2 и найдем ординату (у), y1=9; y2=1. Так точки пересечения двух графиков: (3;9) и (-1; 1).
Запишем ответ x= -1; 3