Поскольку прямая проходит через точку , то подставив её координаты в уравнение прямой получим:
Значит наша прямая имеет вид
В точках пересечения значения функций должны быть равными
По т. Виета: , значит
P.S.: Тут хорошо бы еще отметить, что поскольку в условии заранее известно, что прямая пересекает параболу в двух точках, то проверять условие наличия корней у квадратного уравнения не требуется. Так же, в последней строчке решения, при сокращении дроби на по идее необходимо убедиться что , однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)
На путь из деревни в город, равный 90 км, первый мотоциклист тратит на 18 мин больше, чем второй, поскольку его скорость на 10 км/ч меньше скорости второго. Найдите скорость каждого мотоциклиста.
Объяснение:
Пусть х км/ч - скорость первого мотоциклиста, тогда (х + 10) км/ч - скорость второго мотоциклиста.
Время в пути первого мотоциклиста равно: 90/х.
Время в пути второго мотоциклиста равно: 90/(х + 10).
18 мин = 0,3 ч
Второй корень не подходит, значит, скорость первого мотоциклиста равна 50 км/ч.
Объяснение:
Пусть прямая задается уравнением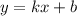
Поскольку прямая проходит через точку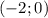 , то подставив её координаты в уравнение прямой получим:
, то подставив её координаты в уравнение прямой получим: 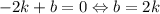
Значит наша прямая имеет вид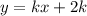
В точках пересечения значения функций должны быть равными
По т. Виета: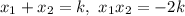 , значит
, значит
P.S.: Тут хорошо бы еще отметить, что поскольку в условии заранее известно, что прямая пересекает параболу в двух точках, то проверять условие наличия корней у квадратного уравнения не требуется. Так же, в последней строчке решения, при сокращении дроби на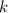 по идее необходимо убедиться что
по идее необходимо убедиться что 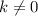 , однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)
, однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)
На путь из деревни в город, равный 90 км, первый мотоциклист тратит на 18 мин больше, чем второй, поскольку его скорость на 10 км/ч меньше скорости второго. Найдите скорость каждого мотоциклиста.
Объяснение:
Пусть х км/ч - скорость первого мотоциклиста, тогда (х + 10) км/ч - скорость второго мотоциклиста.
Время в пути первого мотоциклиста равно: 90/х.
Время в пути второго мотоциклиста равно: 90/(х + 10).
18 мин = 0,3 ч
Второй корень не подходит, значит, скорость первого мотоциклиста равна 50 км/ч.
Скорость второго мотоциклиста равна:
50 + 10 = 60 (км/ч)
ответ: 50 км/ч - скорость 1-ого мотоциклиста;
60 км/ч - скорость 2-ого мотоциклиста.