Поскольку и не превышают единицы по модулю, то для любых натуральных верно . Поэтому , . Складывая оба неравенства, получаем с равенством тогда и только тогда, когда или синус (или косинус) равен нулю, а косинус (или синус +-1) равен 1. Итак, решения следующие: , .
Поскольку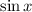 и
и 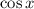 не превышают единицы по модулю, то для любых натуральных
не превышают единицы по модулю, то для любых натуральных 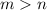 верно
верно 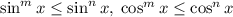 . Поэтому
. Поэтому 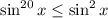 ,
, 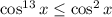 . Складывая оба неравенства, получаем
. Складывая оба неравенства, получаем 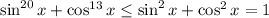 с равенством тогда и только тогда, когда или синус (или косинус) равен нулю, а косинус (или синус +-1) равен 1. Итак, решения следующие:
с равенством тогда и только тогда, когда или синус (или косинус) равен нулю, а косинус (или синус +-1) равен 1. Итак, решения следующие: 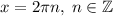 ,
, 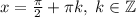 .
.