Пусть (км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в километров, равно часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это часов, минут или же часа = часа. И последний промежуток, часов ( километров со скоростью км/ч).
Теперь, конечно, будем решать уравнение:
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Пусть
(км/ч) - первоначальная скорость мотоциклиста.
Тогда время, за которое он преодолел путь в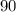
километров, равно 
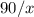часов.
Но, с другой стороны, сумма трех других отрезков времени равна тому же промежутку времени (по условию). Это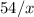
часов, 
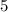минут или же 
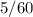часа = 
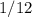часа. И последний промежуток, 
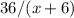часов (
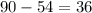километров со скоростью 
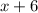км/ч).
Теперь, конечно, будем решать уравнение:
Получилось два корня. Второй доверия не внушает из-за своей отрицательности, так что возьмем исключительно первый.
Первоначальная скорость мотоциклиста -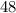
км/ч.
Задача решена!
ответ: 48 км / ч .Это делается так.
Во-первых, нужно рассчитать содержание ЧИСТОЙ кислоты в каждом из растворов (любой водный раствор состоит из чистой кислоты и растворителя).
В 30%-ном растворе массой Х кг содержится 0,30*Х кг чистой кислоты.
В 60%-ном растворе массой Yкг содержится 0,6*Y кг чистой кислоты.
Вода принимается за 0%-ный раствор - она кислоты не содержит.
При смешивании согласно условию задачи
общая масса раствора после смешения равна (X + Y + 10) кг
Чистой кислоты там содержится (0,30*Х + 0,6*Y) кг чистой кислоты.
Таким образом, (0,30*Х + 0,6*Y)/(X + Y + 10) = 0,36 (это первое уравнение системы)
Аналогичным образом составляется второе уравнение и решается система.
Остались вопросы в личку, разберемся.