Все гири имеют различный вес, назовём их в порядке возрастания веса: g₁<g₂<g₃<g₄<g₅. Гири весят натуральное число грамм, поэтому минимальная разница между гирями 1г.
В решении я не буду использовать другие ед. измер., только граммы, поэтому, для упрощения записей, я не буду писать гр.
Пусть минимальный воможный вес для g₁ это x. Тогда: для g₂ - x+1; g₃ - x+2; g₄ - x+3; g₅ - x+4.
Самый минимальный суммарный вес для трёх гирь можно собрать из g₁ , g₂ , g₃ ; а самый максимальный для двух - g₄ , g₅.
Любые три гири весят больше, чем две другие, составим неравество и решим его.
g₁+g₂+g₃>g₄+g₅ ⇒ x+(x+1)+(x+2)>(x+3)+(x+4)
3x+3>2x+7; 3x-2x>7-3; x>4, ⇒ x=5
Получаем, что минимальный суммарный вес для всех гирь 5+(5+1)+(5+3)+(5+4)+(5+5) = 5+6+7+8+9 = 35.
Пусть скорость третьего x км/ч, а время встречи со 2-ым (когда третье догонит второго) t ч. первое уравнение: 20+40t=xt второе уравнение: 25+50(t+1,5)=x(t+1,5)
Вычтем из второго уравнения первое, получим: Выразим из второго уравнения t через x: t=0,15x-8 Подставим в первое уравнение вместо t выражение 0,15x-7,5: 20+40(0,15x-8)=x(0,15x-8) 20+6x-320=0,15x^{2} -8x 0,15x^{2} -14x+300=0 3x^{2}-280x+6000=0 x=(140+-sqrt(19600-18000))/3 x=(140+-40)/3 x=60 или x=100/3 x=100/3 - посторонний корень. Значит, скорость третьего 60 км/ч
Все гири имеют различный вес, назовём их в порядке возрастания веса: g₁<g₂<g₃<g₄<g₅. Гири весят натуральное число грамм, поэтому минимальная разница между гирями 1г.
В решении я не буду использовать другие ед. измер., только граммы, поэтому, для упрощения записей, я не буду писать гр.
Пусть минимальный воможный вес для g₁ это x. Тогда: для g₂ - x+1; g₃ - x+2; g₄ - x+3; g₅ - x+4.
Самый минимальный суммарный вес для трёх гирь можно собрать из g₁ , g₂ , g₃ ; а самый максимальный для двух - g₄ , g₅.
Любые три гири весят больше, чем две другие, составим неравество и решим его.
g₁+g₂+g₃>g₄+g₅ ⇒ x+(x+1)+(x+2)>(x+3)+(x+4)
3x+3>2x+7; 3x-2x>7-3; x>4,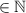 ⇒ x=5
⇒ x=5
Получаем, что минимальный суммарный вес для всех гирь 5+(5+1)+(5+3)+(5+4)+(5+5) = 5+6+7+8+9 = 35.
ответ: 35 грамм.
первое уравнение: 20+40t=xt
второе уравнение: 25+50(t+1,5)=x(t+1,5)
Вычтем из второго уравнения первое, получим:
Выразим из второго уравнения t через x:
t=0,15x-8
Подставим в первое уравнение вместо t выражение 0,15x-7,5:
20+40(0,15x-8)=x(0,15x-8)
20+6x-320=0,15x^{2} -8x
0,15x^{2} -14x+300=0
3x^{2}-280x+6000=0
x=(140+-sqrt(19600-18000))/3
x=(140+-40)/3
x=60 или x=100/3
x=100/3 - посторонний корень.
Значит, скорость третьего 60 км/ч