Решить задачи 1)в разных полуплоскостях относительно прямой AB расположены точки Mи. Докажите, что AM параллельна BN если известно, что AM= BN, AN=BM.
2)Прямая проведенная через вершину В треугольника ABC параллельно стороне AC, образует со
сторонами ВА и ВС равные углы, определить вид треугольника ABC,

Показать ответ

Ответ:

969758676

23.01.2020 08:46

Задача 1:

Нехай теперішній вік брата х років, а сестри - у років. Тоді маємо дві пропорції:

$\frac{x+5}{y+5} =\frac{8}{7}$

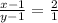
і $\frac{x-1}{y-1} =\frac{2}{1}$

Спростимо першу рівність:

$\frac{x+5}{y+5} =\frac{8}{7}$

7*(х+5)=8*(у+5)

7х+35=8у+35

7х=8х+5

Спростимо другу рівність:

$\frac{x-1}{y-1} =\frac{2}{1}$

х-1=2*(у-1)

х-1=2у-2

х=2у-1

Підставляємо значення х до першої рівності:

7*(2у-1)=8у+5

14у-7=8у+5

6у=12

у=2

Тоді х=2*2-1=3

Отже, теперішній вік брата - 3 роки, вік сестри - 2 роки.

Задача 2:

Треба посадити яблуні у формі п'ятикінечної зірочки. Як на малюнку.

Задача 3:

Нехай кут MAC=х, а кут NBC=у

Сума кутів трикутника 180 °

х+у=90

Трикутники MAC і NBC рівнобічні.

Кут AMC=MCA, відповідно BCN=CNB

AMC=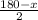 $\frac{180-x}{2}$

BCN=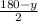 $\frac{180-y}{2}$

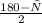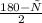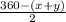
AMC+BCN= $\frac{180-х}{2}$ + $\frac{180-у}{2}$ = $\frac{360-(x+y)}{2}$

Згадуємо, що х+у=90.

Тоді AMC+BCN=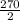 $\frac{270}{2}$ =135

Тоді кут MCN=180-135=45°

Решить олимпиаду1. через п'ять років вік брата буде відноситись до віку сестри як 8: 7. скількироків

0,0(0 оценок)

Ответ:

lololol707lollol

22.05.2022 19:39

Метод Феррари:

уравнение вида

$(1)\ x^4+ax^3+bx^2+cx+d=0$

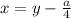
с замены $x=y-\frac{a}{4}$

приводим к виду

$(2)\ y^4+p*y^2+qy+r=0$

где:

$p=b-\frac{3a^2}{8}\\q=\frac{a^3}{8}-\frac{a*b}{2}+c\\r=-\frac{3a^4}{256}+\frac{a^2b}{16}-\frac{a*c}{4}+d$

добавим и вычтем из левой части уравнения 2 выражение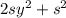 2sy^2+s^2 , где s - некоторое число: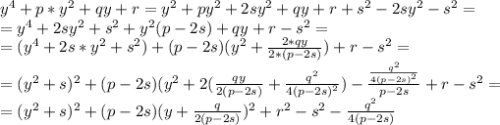 $y^4+p*y^2+qy+r=y^2+py^2+2sy^2+qy+r+s^2-2sy^2-s^2=\\=y^4+2sy^2+s^2+y^2(p-2s)+qy+r-s^2=\\=(y^4+2s*y^2+s^2)+(p-2s)(y^2+\frac{2*qy}{2*(p-2s)})+r-s^2=\\=(y^2+s)^2+(p-2s)(y^2+2(\frac{qy}{2(p-2s)}+\frac{q^2}{4(p-2s)^2})-\frac{\frac{q^2}{4(p-2s)^2}}{p-2s}+r-s^2=\\=(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2+r^2-s^2-\frac{q^2}{4(p-2s)}$

получим:

$(3)\ (y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2+r^2-s^2-\frac{q^2}{4(p-2s)}=0$

Пусть s - корень уравнения

$(4)\ r^2-s^2-\frac{q^2}{4(p-2s)}=0$

Тогда уравнение 3 примет вид:

$(5)(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2=0$

Избавляемся в уравнении 4 от знаменателя:

$r(p-2s)-s^2(p-2s)-\frac{q^2}{4}=0$

Раскроем скобки и получим:

$(6)\ 2s^3-ps^2-2rs+rp-\frac{q^2}{4}=0$

Уравнение 6 называется кубической резольвентой уравнения 4 степени.

Разложим уравнение 5 на множители:

$(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2=0\\(y^2+s)^2-(2s-p)(y-\frac{q}{2(2s-p)})^2=0\\(y^2+s^2)^2-(y*\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}})^2=0\\(y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s)(y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s)=0$

Получим два квадратных уравнения:

$(7)\ y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s=0\\(8)\ y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s=0$

Применяем этот метод для решения уравнения:

$x^{4} -4x^{3} -51x^{2} +306x-432=0$

коэффициенты:

a=-4

b=-51

c=306

d=-432

Определяем p,q и r:

$p=b-\frac{3a^2}{8}=-51-\frac{3*4^2}{8}=-57 \\q=\frac{a^3}{8}-\frac{a*b}{2}+c=\frac{(-4)^3}{8}-\frac{-4*(-51)}{2}+306=196 \\r=-\frac{3a^4}{256}+\frac{a^2b}{16}-\frac{a*c}{4}+d=-\frac{3*2^8}{256} +\frac{16*(-51)}{16} -\frac{(-4)*306}{4} -432=-180$

Ищем s:

$2s^3+57s^2+360s+57*180-\frac{196^2}{4}=0\\2s^3+57s^2+360s+656=0\\P(s)=2s^3+57s^2+360s+656\\s=-1\Rightarrow P(-1)=-2+57-360+656\neq 0\\s=-2\Rightarrow P(-2)=-2*8+57*4-360*2+656=148\neq 0\\s=-4\Rightarrow P(-4)=-2*4^3+57*16-360*4+656=0 \Rightarrow s_1=-4$

Возможно, у этого уравнения третьей степени есть и другие действительные корни. Но для данной задачи находить их все не обязательно. Достаточно одного корня, т.е числа, при котором выражение обращается в ноль.

Подставляем p,q,r и s в квадратные уравнения 7 и 8:

$y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s=0\\y^2-y\sqrt{-8+57}+\frac{196}{2\sqrt{-8+57}} -4=0\\y^2-7y+10=0\\D=49-40=9=3^2\\y_1=\frac{7+3}{2}=5\\y_2=\frac{7-3}{2}=2$

$y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s=0\\y^2+y\sqrt{-8+57}-\frac{196}{2\sqrt{-8+57}} -4=0\\y^2+7y-18=0\\D=49+72=121=11^2\\y_3=\frac{-7+11}{2}=2\\y_4=\frac{-7-11}{2}=-9$