fнаиб = 4; f наим = 0
Объяснение:
28б
f(x) = x³ - 6x² + 9x при х ∈ [0; 3]
Значения функции на концах интервала
f(0) = 0
f(3) = 27 - 54 + 27 = 0
Производная функции
f'(x) = 3x² - 12x + 9
Точки экстремумов
3x² - 12x + 9 = 0
х² - 4х + 3 = 0
D = 16 - 12 = 4 = 2²
x₁ = 0.5(4 - 2) = 1
x₂ = 0.5 (4 + 2) = 3
В точке х₁ = 1 находится локальный максимум
f(1) = 1 - 6 + 9 = 4 - максимальное значение
В точке х₂ = 3 находится локальный минимум
f(3) = 0
Сравнивая со значениями функции на границах интервала, делаем вывод. что наибольшее значение функции на заданном интервале равно 4. наименьшее равно 0.
Покажу один из сопособов решения таких неравенств
1) проверим ограничения
2) введем замену
получаем,
А далее самое интересное
будем делить многочлен на многочлен
_t²-16t+30 | t-2 и _t²-7t+3 | t-7
t²-2t ______ t²-7t _____
_____ t-14 ____ t
_ -14t+30 3 (остаток)
-14t+28
------------
2 (остаток)
тогда
теперь все совсем просто
решаем методом интервалов
__-____ 2 ___+____4___-____7___+____
Не забываем проверить ограничение
ответ (-∞; 1)∪[2; log₂7)
fнаиб = 4; f наим = 0
Объяснение:
28б
f(x) = x³ - 6x² + 9x при х ∈ [0; 3]
Значения функции на концах интервала
f(0) = 0
f(3) = 27 - 54 + 27 = 0
Производная функции
f'(x) = 3x² - 12x + 9
Точки экстремумов
3x² - 12x + 9 = 0
х² - 4х + 3 = 0
D = 16 - 12 = 4 = 2²
x₁ = 0.5(4 - 2) = 1
x₂ = 0.5 (4 + 2) = 3
В точке х₁ = 1 находится локальный максимум
f(1) = 1 - 6 + 9 = 4 - максимальное значение
В точке х₂ = 3 находится локальный минимум
f(3) = 0
Сравнивая со значениями функции на границах интервала, делаем вывод. что наибольшее значение функции на заданном интервале равно 4. наименьшее равно 0.
Покажу один из сопособов решения таких неравенств
1) проверим ограничения
2) введем замену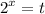
получаем,
А далее самое интересное
будем делить многочлен на многочлен
_t²-16t+30 | t-2 и _t²-7t+3 | t-7
t²-2t ______ t²-7t _____
_____ t-14 ____ t
_ -14t+30 3 (остаток)
-14t+28
------------
2 (остаток)
тогда
теперь все совсем просто
решаем методом интервалов
__-____ 2 ___+____4___-____7___+____
Не забываем проверить ограничение
ответ (-∞; 1)∪[2; log₂7)