Пусть v ( можно х ) - скорость первой машины , тогда скорость 2 машины ( v+20). Путь они одиннаковый 180км, выразим время движения 1 и 2 машины. t1=180 / x , t2=180 / ( x+20) . Зная , что первая пришла позже на 45 мин=0,75ч , составим уравнение: 180 / x - 180 / ( x+20)=0,75 , решим уравнение относительно х. 180х+3600 - 180х =0,75х^2 +15x , получили квадратное уравнение 0,75х^2 +15x -3600=0 , решаем , получаем 2 корня х1=60 , х2= -80 ( скорость отрицательной не бывает ) значит скорость 1 автомобиля v=60км/ч , скорость второго 60+20=80км/ч . ответ: 1 машина 60км/ч , 2 машина 80км /ч.
Пусть v ( можно х ) - скорость первой машины , тогда скорость 2 машины ( v+20).
Путь они одиннаковый 180км, выразим время движения 1 и 2 машины.
t1=180 / x , t2=180 / ( x+20) . Зная , что первая пришла позже на 45 мин=0,75ч , составим уравнение: 180 / x - 180 / ( x+20)=0,75 , решим уравнение относительно х.
180х+3600 - 180х =0,75х^2 +15x , получили квадратное уравнение
0,75х^2 +15x -3600=0 , решаем , получаем 2 корня х1=60 , х2= -80 ( скорость отрицательной не бывает ) значит скорость 1 автомобиля v=60км/ч , скорость второго 60+20=80км/ч .
ответ: 1 машина 60км/ч , 2 машина 80км /ч.
1) Если углы в условии заданы в градусах
187° = 90° + 90° + 7° - третья четверть : sin 187° < 0
215° = 90° + 90° + 35° - третья четверть : cos 215° < 0
80° - первая четверть : tg 80° > 0
=======================================
2) Если углы в условии заданы в радианах. Полный оборот 2π≈6,28318 радиан, одна четверть π/2≈1,5708 радиан.
187 ≈ 29 · 2 · 3,14159 + 3 · 1,5708 + 0,07538 ≈
29 полных оборотов, четвёртая четверть : sin 187 < 0
215 ≈ 34 · 2 · 3,14159 + 1,37188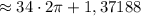
34 полных оборота, первая четверть : cos 215 > 0
80 ≈ 12 · 2 · 3,14159 + 3,14159 + 1,46025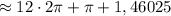
12 полных оборотов, третья четверть : tg 80 > 0