решите квадратное неравенства​

Так, ну смотрите. Они просто обрезали решение. Если решать подробнее, то получается вот так:

Минус перед первой дробью мы можем поставить в числитель, сути это не поменяет. Приводим слагаемые к общему знаменателю, для этого домножаем второе на :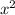

При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитается числитель второй дроби, а знаменатель остаётся прежним.

Дробь равна нулю тогда, когда её числитель равен нулю, а знаменатель отличен от нуля, этот нюанс в приложенном решении учтён. Приравниваем числитель к нулю:

Ну и далее уже как на картинке.

а)sin2x \ (1 + ctgx) = 0;

По основному свойству дроби: числитель дроби равен, а знаменатель не равен нулю. Тогда получим систему из двух уравнений:

sin2x = 0 и (1 + ctgx) ≠ 0;

Решаем отдельно каждое из них:

1) 1 + ctgx ≠ 0;

ctgx ≠ -1;

x ≠ -arcctg(1) + ╥K, K є Z;

x ≠ -╥ / 4 + ╥K, K є Z;

2) sin2x = 0;

2x = ╥k, K є Z;

x = ╥k / 2, K є Z;

Так как полученные решения не совпадают с ограничениями уравнения, то можем записать ответ.

ответ: x = ╥k / 2, K є Z.

б)Раскроем скобки. Для этого будем использовать формулы приведения:

cosx+cosx-cosx=0.

В полученном выражении есть два слагаемых одинаковых, но разные по знаку, в сумме они дают 0, поэтому:

cosx=0.

Это уравнение представляет собой частный случай:

x=п/2+пn, n принадлежит Z.

ответ: п/2+пn, n принадлежит Z.