решите любой номер, кроме 1, 3 и 6

1)  h =13m;     2) t =1+ √1,3+

Объяснение:

h = 18t - 5t²  

вначале  при полете вверх на камень действует сила тяжести, которая снижает его скорость до  полной остановки, а затем он под действием силы тяжести вернется обратно на землю.

1) определим в какой момент времени камень брошенный вверх потеряет скорость (v=0)

v = v0 - gt ;        v0-gt = 0

t = v0/g    время подъема,     t = 10/10 =1 c.

а теперь рассчитаем высоту на которую он поднимется  

h = 18v0/g - 5(v0/g)²         (для удобства расчета примем  g=10)

h = 18*10/10 - 5(10/10)² =18 - 5 =13

h =13 m         t = 1 время подъема

2)теперь определим время возврата мяча на землю под действием силы тяжести.

h = v0t + gt²;   где   v0=0 начальная скорость.  g =10

h = gt²

t² = h/g

 время падения

полное время полета с момента запуска

t = t1 + t2 = 1 + √1.3

ответ:   y= -3x+11  .

Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая:    .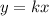

Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент  k  .

Линейная функция задаётся уравнением    .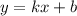  

Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид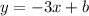  

 Найдём число  "b"  , подставив координаты точки D(7;-10)  в уравнение линейной функции.