Это сложные функции. К примеру на первой: 1.y=tg(x/3+10). y=f(t), где t=g(x). В данном случае f(t)=tg(x/3+10), а g(x)=x/3+10. Т.к. производная f'(t)=1/cos^2(t), а g'(x)=1/3+10, то за теоремой про производную сложной функции(y'(x)=f'(t)*g'(x), если кратко, то брать производную главной функции(тангенса) и умножать на производную того, что в нём) y'(x)=(1/cos^2(x/3+10) )* 1/3 = 1/3cos^2(x/3+10). 2. Аналогично: f'(x)=-sin(3-2x)*(3-2x)'=-sin(3-2x)*(-2)=2sin(3-2x). 3.tgx*sin(2x+5). Общий вид: (f*g)'=f'g+f*g'. Т.е.:(tgx)'*sin(2x+5) + (sin(2x+5))'*tgx=(1/cos^2(x))*sin(2x+5) + 2cos(2x+5)*tgx=sin(2x+5)/cos^2(x) + 2cos(2x+5)*tgx. (2я перед косинусом появилась из-за того, что это сложная функция, которую я описал ранее). Расписываем tgx как sinx/cosx, получаем sin(2x+5)/cos^2(x) + (2cos(2x+5)*sin(x))/cos(x). Сводим к общему знаменателю cos^2(x) = (sin(2x+5) + 2cos(2x+5)*sin(x)*cos(x))/cos^2(x)=(sin(2x+5)+cos(2x+5)*sin2x)/cos^2(x), т.к. 2*sin(x)*cos(x)=sin2x. Всё, вроде бы. Надеюсь, что понятно. :)
См объяснение
Объяснение:
а) так как перед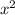
стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
б) координаты вершины (x0, y0) вычисляются по формуле:
x0 =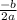
= 
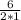= 3
y0 = y(x0) = 9 - 6*3 +5 = -4
Значит, координаты вершины : (3, -4)
c) Ось симметрии задается уравнением: x = 3
d) По теореме Виета:
Если x1, x2 - корни квадратного уравнения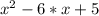
, ТО
Отсюда получаем корни x1 = 1; x2 = 5
Эти корни и есть нули функции
e) Дополнительные точки можно найти путем подстановки любых чисел: например, пусть x=0. тогда y = y(0) = 5
f) см прикрепленный рисунок
1.y=tg(x/3+10). y=f(t), где t=g(x). В данном случае f(t)=tg(x/3+10), а g(x)=x/3+10. Т.к. производная f'(t)=1/cos^2(t), а g'(x)=1/3+10, то за теоремой про производную сложной функции(y'(x)=f'(t)*g'(x), если кратко, то брать производную главной функции(тангенса) и умножать на производную того, что в нём) y'(x)=(1/cos^2(x/3+10) )* 1/3 = 1/3cos^2(x/3+10).
2. Аналогично: f'(x)=-sin(3-2x)*(3-2x)'=-sin(3-2x)*(-2)=2sin(3-2x).
3.tgx*sin(2x+5). Общий вид: (f*g)'=f'g+f*g'. Т.е.:(tgx)'*sin(2x+5) + (sin(2x+5))'*tgx=(1/cos^2(x))*sin(2x+5) + 2cos(2x+5)*tgx=sin(2x+5)/cos^2(x) + 2cos(2x+5)*tgx. (2я перед косинусом появилась из-за того, что это сложная функция, которую я описал ранее). Расписываем tgx как sinx/cosx, получаем sin(2x+5)/cos^2(x) + (2cos(2x+5)*sin(x))/cos(x). Сводим к общему знаменателю cos^2(x) = (sin(2x+5) + 2cos(2x+5)*sin(x)*cos(x))/cos^2(x)=(sin(2x+5)+cos(2x+5)*sin2x)/cos^2(x), т.к. 2*sin(x)*cos(x)=sin2x. Всё, вроде бы. Надеюсь, что понятно. :)