Решите подстановки систему линейных уравнений
11х+3у=20
5х-6у=14
Решите подстановки систему уравнений
2х-у=-1
ху=15
В данной системе уравнений и в трёх следующих заданиях решением системы является две пары чисел, ответ записывать следующим образом (2; 7); (4; 5)
Решите подстановки систему уравнений
х-18у=6
ху=4.
Объяснение:
Построим график
Пусть S площадь ограниченная графиком функции осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
Координаты точек A и B:
A(0;-4)
B(2;0)
Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).
Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде: .
.
Пусть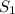 - площадь между прямой
- площадь между прямой 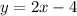 и функцией
и функцией 
Пусть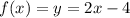 и
и  .
.
По формуле площади прямоугольного треугольника:
Промежуток интегрирования:![[0;2]](/tpl/images/4566/3708/2ae13.png)
Докажем, что при
при ![x \in [0;2]](/tpl/images/4566/3708/4a92d.png)
По теореме:
ответ
Объяснение:
1) 3 1/9 : 2 1/3 - 2 5/6=28/9 : 7/3 -2 5/6=28/9*3/7 -2.5/6=4/3-2 5/6=
=8/6-2 5/6=-(2 5/6 -1 2/6)=-1 3/6=-1 1/2 = -1.5;
2) 1 5/7 - 4 3/13 : 1 19/26 = 1 5/7 - 55/13 : 45/26=1 5/7-55/13*26/45 =
=1 5/7-22/9 = 1 5/7 - 2 4/9 = -(2 28/63-1 45/63) = - (1 (28-45)/63)=
=-(63+28-45)/63= -46/63;
3) 10 16/17 : 8 5/11 + 1 2/3 = 186/17 : 93/11 +1 2/3 = 186/17 * 11/93 + 1 2/3 =
=22/17+1 2/3=1 5/17+1 2/3=1 15/51 + 1 34/51 = 2 49/51;
4) 47/48 : 3 13/27 - 13/16= 47/48 : 94/27 - 13/16 = 47/48*27/94 -13/16=
= 27/96-13/16 = 27/96-78/96=-51/96=-17/32.