Решите пример по действиям.
​

Ну насчет степеней ты сам догадался, про замену тебе подсказали, решаем дальше.
Во-первых, t = (2+√3)^x > 0 при любом x
t^3 - 5t^2 + 6t + 1/t - 5 = 0
Умножаем все на t.
t^4 - 5t^3 + 6t^2 - 5t + 1 = 0
Это симметричное уравнение, оно решается делением на t^2
t^2 - 5t + 6 - 5/t + 1/t^2 = 0
Заметим, что (t + 1/t)^2 = t^2 + 2*t*1/t + 1/t^2 = (t^2 + 2 + 1/t^2)
(t^2 + 2 + 1/t^2) - 5(t + 1/t) + 4 = 0
(t + 1/t)^2 - 5(t + 1/t) + 4 = 0
Опять замена t + 1/t = z >= 2 при любом t > 0, причем z = 2 при t = 1.
z^2 - 5z + 4 = 0
Наконец-то свели к к квадратному уравнению.
(z - 1)(z - 4) = 0
1) z = 1 - не бывает, решений нет
2) z = 4 = t + 1/t
t^2 - 4t + 1 = 0
D = 4^2 - 2*1*1 = 16 - 4 = 12 = (2√3)^2
t1 = (4 - 2√3)/2 = 2 - √3
t2 = 2 + √3
Обратная замена
t1 = (2 + √3)^x = 2 - √3 = (2 + √3)^(-1); x1 = -1
t2 = (2 + √3)^x = 2 + √3; x2 = 1
Всё!

Объяснение:

1. а)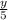 ∈{-2,-1} ⇒ y∈{-10,-5} (условие выполняется)

б)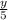 ∈{0}, тогда 0<1, но 0<3 ⇒ противоречие  

в)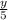 ∈{-5, -1}, y∈{-10,-5}

г)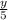 ∈{15}, y∈{75}, но y<5 ⇒ противоречие

2. a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12}

a) a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12}

б) a∈{5,6,7}, b∈{9,10,11,}, a+b∈{14,15,16}

в) a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12} a+b∈{14,15,16,17,18}  

3. A) a>0

б) a < 0

в) a-8 (всегда) < a + 8 ⇒ противоречие

г) при возведение в квадрат любого числа получится положительное ⇒ когда мы поменяем его на отрицательный после возведения, полученное значение будет < 0. Но при возведение 0^2 = 0 ⇒ a=3 единственное решение.

4. p ∈ {10, 11, 12, 13}

а) если p ∈ {10, 11, 12, 13}(по условию), то выполняется только одно из условий ⇒ противоречие

б) p ∈ {10, 11, 12, 13}

в) значение всех трех дробей должно быть отрицательным чтобы соблюдалось условие, но так как >0 приходим у противоречию

г) аналогично в

5. а), в)

6. x - а), в), г)

y - б)