Для того чтобы решить квадратное неравенство мы первом делом приравниваем его к нулю и решаем как квадратное уравнение, то есть:
а)
Далее отмечаем эти две точки на координатной прямой и определяем знак на одном из её участков. Я возьму средний участок, а конкретнее число 0 (оно же из среднего участка). Подставлю в уравнение: 2*0-7*0-9, число получу отрицательное, значит на этом промежутке ставлю знак "-". При переходе через корень уравнения( в нашем случае -1 и 4,5) нак меняется на противоположный, то есть на концах воординатной прямой мы получим два плюса.
Смотрим на знак неравенсва: нам нужен участок меньший 0, то есть отрицательный, значит ответ (-1; 4,5). Скобки круглые так как неравенство строгое.
Аналогично далее:
б)
х1= -7
х2=+7
Отметим на числовой прямой и определим знак, я сново подствлю 0 (из центрального интервала) и получая отрицательное число, значит положительные знаки(а они нам и нужны) мы получим на концах данной числовой прямой: (-∞;-7)∪(7;+∞)
в)
Значит пересечения с осью нет, ветви положительные и парабола находится над числовой прямой. Так как у нас в неравенстве знак "больше", то вопрос заключается в том, при каком х парабола находится выше прямой ох. В нашем случае при любом х.
а)(-1; 4,5)
б) (-∞;-7)∪(7;+∞)
в) любые х
Объяснение:
Для того чтобы решить квадратное неравенство мы первом делом приравниваем его к нулю и решаем как квадратное уравнение, то есть:
а)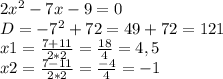
Далее отмечаем эти две точки на координатной прямой и определяем знак на одном из её участков. Я возьму средний участок, а конкретнее число 0 (оно же из среднего участка). Подставлю в уравнение: 2*0-7*0-9, число получу отрицательное, значит на этом промежутке ставлю знак "-". При переходе через корень уравнения( в нашем случае -1 и 4,5) нак меняется на противоположный, то есть на концах воординатной прямой мы получим два плюса.
Смотрим на знак неравенсва: нам нужен участок меньший 0, то есть отрицательный, значит ответ (-1; 4,5). Скобки круглые так как неравенство строгое.
Аналогично далее:
б)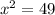
х1= -7
х2=+7
Отметим на числовой прямой и определим знак, я сново подствлю 0 (из центрального интервала) и получая отрицательное число, значит положительные знаки(а они нам и нужны) мы получим на концах данной числовой прямой: (-∞;-7)∪(7;+∞)
в)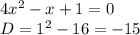
Значит пересечения с осью нет, ветви положительные и парабола находится над числовой прямой. Так как у нас в неравенстве знак "больше", то вопрос заключается в том, при каком х парабола находится выше прямой ох. В нашем случае при любом х.
чтобы решить уравнение нужно привести всё к общему знаменателю
х 7 8
___ - =
х-2 х + 2 х² - 4
нижний знаменатель х² - 4 можно разложить по формуле разности квадрата. вы её наверняка проходили.
получится (х-2)(х+2)
всё уравнение имеет вид
х 7 8
___ - =
х-2 х + 2 (х-2)(х+2)
ну а теперь домножаем до одного знаменателя. в первом столбике умножим на (х+2), во втором на (х-2), а третий так и оставим.
получится:
х(х+2) - 7(х-2) - 8
= 0;
(х-2)(х+2)
когда раскроем скобки получится:
х² + 2х - 7х + 14 - 8
= 0;
(х-2)(х+2)
сверху получится х² - 5х + 6 = 0
находим через дискриминант. D = b² - 4ac;
D = 25 - 4*6 = 25-24 = 1;
х₁= -b + √D
= 5 + 1
2a 2
x₁ = 3;
х₂ = 5-1
___ = 2
2
всё уравнение имеет вид
(x-2)(x-3)
= 0;
(х-2)(х+2)
сократив дробь получим
х-3
___ = 0;
х + 2
т.к. делить на ноль нельзя, то х+2 ≠0
х ≠ -2
ответ: х∋(-∞;-2)(-2;+∞)
на самом деле это несложное уравнение, просто я пыталась как можно больше объяснить свои действия :)