Данное неравенство является квадратным, тогда, для начала решаем левую часть как обычное квадратное уравнение.
D=1-4*0.25=1-1=0
z=-=-1
Зададим функцию вида y=+bx+c
В итоге, окончательная функция -- y=+z+0.25
Так как, +, тогда ветки параболы будут направлены вверх.
Рисуем график с центром в точке -1.
По условию, нам надо отрезок, который меньше нуля, т.е. ниже плоскости, но мы видим, что график находиться над функцией, тем самым делаем вывод, что неравенство значений не имеет.
ответ: a∈ [-3;10]
Объяснение:
x^4-2x^3-12x^2+20x+20-2ax+8a-a^2=0
x^4-2*x^3-12*x^2 +20*x +20 - ( a^2 +2*a*(x-4) ) = 0
x^4-2*x^3-12*x^2 +20*x +20 +(x-4)^2 -(a^2+2*a*(x-4) +(x-4)^2)=0
(x-4)^2= x^2 -8*x+16
x^4-2*x^3-11*x^2 +12*x +36 - (a+x-4)^2= 0
x^4+x^2 +6^2 + 2*x^2*(-x) + 2*x^2*(-6) +2*(-x)*(-6) -(a+x-4)^2=0
Видна формула квадрата суммы трех слагаемых :
(a+b+c)^2= a^2+b^2+c^2 +2*ab+2*ac +2*bc
x^4+x^2 +6^2 + 2*x^2*(-x) + 2*x^2*(-6) +2*(-x)*(-6)
(x^2-x-6)^2 = x^4+x^2 +6^2 + 2*x^2*(-x) + 2*x^2*(-6) +2*(-x)*(-6)
Таким образом уравнение имеет вид :
(x^2-x-6)^2 -(a+x-4)^2=0
(x^2-2x-2 -a)*(x^2-10+a)=0
Разбивается на два подуравнения :
1 ) (x-1)^2= a+3
2) x^2 = 10-a
Данное уравнение имеет не менее 3 корней , когда :
1) Оба уравнения имеют по два решения .
2) Первое уравнение имеет 1 решение , а второе 2
3) Наоборот случаю 2
1 cлучай :
a+3>0
10-a>0
a∈ ( -3 ;10)
2 cлучай :
a=-3
a<10 (верно)
3 cлучай :
a=10
a>-3 (верно)
Таким образом ответ :
a∈ [-3;10]
∅ -- решений нет
Объяснение:
Данное неравенство является квадратным, тогда, для начала решаем левую часть как обычное квадратное уравнение.
D=1-4*0.25=1-1=0
z=-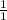
=-1
Зададим функцию вида y=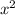
+bx+c
В итоге, окончательная функция -- y=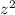
+z+0.25
Так как, +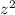
, тогда ветки параболы будут направлены вверх.
Рисуем график с центром в точке -1.
По условию, нам надо отрезок, который меньше нуля, т.е. ниже плоскости, но мы видим, что график находиться над функцией, тем самым делаем вывод, что неравенство значений не имеет.