Так как значение функции в точке минимума на интервале (-2;2) больше, чем правосторонний предел функции в точке х= -2, и , точка х= -2 не входит в исследуемый промежуток , то наименьшего значения функции найти нельзя. Значения функции ограничены снизу величиной (-2) .
Кстати, нельзя в этом случае найти и наибольшего значения функции на интервале (-2;2), так как
. Значения функции ограничены сверху величиной 10 .
Смотри график.
Если по условию надо найти наименьшее значение функции на сегменте [-2;2 ] , то решение написано ниже.
Здесь пытаемся представить выражение т.о., чтобы основание и число под знаком логарифма совпадали, как то ㏒₂2, ㏒₅5. Зачем? Затем, что ㏒₂2=1; ㏒₅5=1. затем применяем правило ㏒₂⁻¹2² , с которого избавляемся от степеней, надо верхний показатель степени, т.е. 2 разделить на показатель основания, т.е. -1, получим 2/(-1)=-2, и эта -2*1=-2, аналогично другой логарифм.
далее, 0.25=1/4=2⁻²
㏒₀.₂₅2=㏒₂₋²2¹ =1/(-2)㏒₂2=(-1/2)*1=-1/2=-0.5 - та же схема. добились, что в основании 2⁻², под логарифмом тоже 2¹, и показатели разделили.
Так как значение функции в точке минимума на интервале (-2;2) больше, чем правосторонний предел функции в точке х= -2,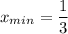 и
и 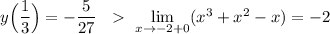 , точка х= -2 не входит в исследуемый промежуток , то наименьшего значения функции найти нельзя. Значения функции ограничены снизу величиной (-2) .
, точка х= -2 не входит в исследуемый промежуток , то наименьшего значения функции найти нельзя. Значения функции ограничены снизу величиной (-2) .
Кстати, нельзя в этом случае найти и наибольшего значения функции на интервале (-2;2), так как
Смотри график.
Если по условию надо найти наименьшее значение функции на сегменте [-2;2 ] , то решение написано ниже.
㏒₅0.2+㏒₀.₅4=㏒₅(1/5)+㏒₍₁/₂₎2²=㏒₅5⁻¹+㏒₂⁻¹2²=-1*㏒₅5-(2/1)㏒₂2=-1*1-2*1=
-3
Здесь пытаемся представить выражение т.о., чтобы основание и число под знаком логарифма совпадали, как то ㏒₂2, ㏒₅5. Зачем? Затем, что ㏒₂2=1; ㏒₅5=1. затем применяем правило ㏒₂⁻¹2² , с которого избавляемся от степеней, надо верхний показатель степени, т.е. 2 разделить на показатель основания, т.е. -1, получим 2/(-1)=-2, и эта -2*1=-2, аналогично другой логарифм.
далее, 0.25=1/4=2⁻²
㏒₀.₂₅2=㏒₂₋²2¹ =1/(-2)㏒₂2=(-1/2)*1=-1/2=-0.5 - та же схема. добились, что в основании 2⁻², под логарифмом тоже 2¹, и показатели разделили.