Решите систему уравнений:

x^2+y√xy=72

y^2+x√xy=36

кубическая функция может иметь только локальный минимум. Потому что при х ->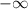 она уходит в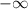

точки минимума и максимума соответствуют нулям производной

сумма степеней равна нулю, значит один корень = 1, второй = a

локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)

значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7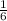

при а>1 локальный минимум f(x=a) = a^3/3-(a+1)/2*a^2+a^2 - 7 = (1/3 - 1/2) a^3 + (-1/2+1) a^2 - 7 = - a^3 / 6 + a^2 / 2 - 7

при a = 1 имеем точку перегиба и никакого минимума

ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г

Объяснение:

1. Найдите значение алгебраической дроби 2х/х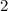-1, при х= 1/3

• а) 0,75; б) -0,75 ; в) - ;г) -1,5

2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла

а)4 б)-2 в) -4 г) нет таких значений

3. Какое из предложенных выражений записано в виде алгебраической дроби?

а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х

4. Найдите значение выражения , при а= -0,7, в=0,3

а)2,5; б) -2,5; в) 1; г) другой ответ.

5.При каком значении а дробь не определена?

а) 0; б) - ; в) ; г)другой ответ.

6. Найди допустимые значения букв, входящих в дробь  а/b

а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа  

7.Выберите дробно- рациональные выражения 2х/3+4/7,  2-5х/7,3, 3/х-2

а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2