Решите тригонометрическое уравнение: 2sin2x-√2=0

1) a)y=3 б)x=3   в)  (3;+∞) возрастает (-∞;3) убывает

2)а)у=-0,5 б) у=0,25 в) у=3

3) у(4)>y(3)                y(-3)>y(-2)                         y(2)<y(-5)

Объяснение:

1) находим по графику абсцисса -это х ордината это -у

2)подставляем вместо х значение и считаем

3) a)у(4)=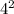=16         б)у(-3)=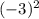=9                   в)   у(2)=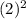=4

    у(3)=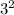=9                у(-2)=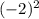=4                          у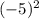(-5)==25    

    у(4)>y(3)                    y(-3)>y(-2)                                     y(2)<y(-5)

Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии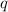 должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.

Графически это выглядит так: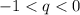 или .

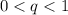Рассмотрим наши примеры:

1)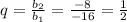 . Выполняются ли условия неравенства?

. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.

2)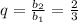 . Выполняются ли условия неравенства?

. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.

3)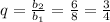 . Выполняются ли условия неравенства?

. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.