То либо имеют одинаковые знаки, либо один из них равен , но поскольку нас интересует наибольшее значение: , то целесообразно рассматривать:
Откуда, с учетом ОДЗ имеем:
Поскольку левая и правая часть равенства положительны, то после возведения в квадрат получаем равносильное уравнение ( в данном случае все радикалы не могут быть одновременно равны , также не трудно заметить, что удвоенные произведения в левой и правой части одинаковы и равны , поэтому они уничтожаться)
Откуда, получим:
Применим такой хитрый прием, вычтем из обеих частей равенства удвоенное произведение , но тогда слева и справа имеем квадрат разности:
Оно равносильно совокупности двух уравнений:
То есть уравнение:
равносильно совокупности двух уравнений, что представлены выше.
То есть, у него с каждым из двух уравнений выше есть общие корни.
Причем, в сумме эти общие корни дают множество корней исходного уравнения.
Cложим исходное уравнение с первым:
В полученном уравнении некоторые зависимости совпадают с зависимостями в исходном уравнении, причем хотя бы одна зависимость подойдет.
Сложим исходное уравнение со вторым:
То есть, если уравнение имеет корни, то их надо искать из множества:
Все корни подходят по ОДЗ.
Подставим :
Пара подходит и рассматривать дальнейшие пары нет смысла, ибо
- наибольшее из возможных, а - наибольшее из возможных.
ответ: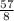
Объяснение:
Поскольку:
То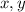
либо имеют одинаковые знаки, либо один из них равен 
, но поскольку нас интересует наибольшее значение: 
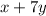, то целесообразно рассматривать:
Откуда, с учетом ОДЗ имеем:
Поскольку левая и правая часть равенства положительны, то после возведения в квадрат получаем равносильное уравнение ( в данном случае все радикалы не могут быть одновременно равны
, также не трудно заметить, что удвоенные произведения в левой и правой части одинаковы и равны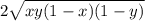 
, поэтому они уничтожаться)
Откуда, получим:
Применим такой хитрый прием, вычтем из обеих частей равенства удвоенное произведение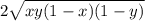
, но тогда слева и справа имеем квадрат разности:
Оно равносильно совокупности двух уравнений:
То есть уравнение:
равносильно совокупности двух уравнений, что представлены выше.
То есть, у него с каждым из двух уравнений выше есть общие корни.
Причем, в сумме эти общие корни дают множество корней исходного уравнения.
Cложим исходное уравнение с первым:
В полученном уравнении некоторые зависимости совпадают с зависимостями в исходном уравнении, причем хотя бы одна зависимость подойдет.
Сложим исходное уравнение со вторым:
То есть, если уравнение имеет корни, то их надо искать из множества:
Все корни подходят по ОДЗ.
Подставим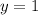
:
Пара подходит и рассматривать дальнейшие пары нет смысла, ибо
Таким образом, наибольшее значение:
Стороны прямоугольника: длина 15 см, ширина 7 см
Объяснение:
Дано:
Прямоугольник со сторонами а₁ - длина и b - ширина
Р₁ = 44 см
a₂ = a₁ - 5 см
S₂ = S₁ - 35 cм²
Найти:
а₁ и b - стороны прямоугольника
Периметр исходного прямоугольника
Р₁ = 2 (а₁ + b)
44 = 2 (а₁ + b)
а₁ + b = 22
откуда
a₁ = 22 - b (1)
Площадь исходного прямоугольника
S₁ = а₁ · b
Площадь уменьшенного прямоугольника
S₂ = (a₁ - 5)· b и S₂ = а₁ · b - 35
(a₁ - 5)· b = а₁ · b - 35
а₁ · b - 5b = а₁ · b - 35
5b = 35
b = 7 (см)
Подставим в (1)
а₁ = 22 - 7 = 15 (см)